Shigeru Yoshikawa (011-81-468-41-1248)
3-12-2-6304 Nagase
Yokosuka, 239 Japan
Popular version of paper 5pMU9
Presented Friday afternoon, December 6, 1996
3rd Joint ASA/ASJ Meeting, Honolulu, Hawaii
Embargoed until 6 December 1996
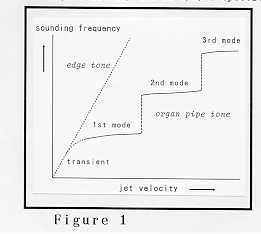
The physics of the organ pipe sounding mechanism is still challenging in spite of its long research history back to the pioneering works of Helmholtz and Rayleigh. The organ pipe shows the sounding characteristics as depicted in Fig. 1. The sounding frequency depends on the velocity (or the blowing pressure) of the jet issued from the flue slit, and the stable frequency range for playing is restricted to a region of proper jet velocities. This relation between the jet velocity and the resulting tone frequency in the steady-state oscillation is well understood and established by many theoretical and experimental investigations.
However, there remain essential problems unsolved: (1) How is the sounding amplitude determined in the steady state? (2) How is the organ pipe tone delivered from the transient state by splitting off from the edge tone? (3) What is the physical substance stimulating and sustaining the sounding process throughout? These problems have been attacked by several researchers, and at present we have borne a conclusion that the wavy motion of the jet and its interaction with the associated vortex should be responsible for them.
This paper is a first-stage effort to draw a more definite understanding of them. Blowing experiments were carried out the visualize the behavior of the smoked jet over the mouth opening between the flue and the edge. A digital high-speed video camera (1297 frames per second) was used to capture and record instantaneous shapes of the jet. Concerning the problem (1) above, determination of the spatial amplification factor of the jet wave is essential. On the other hand, in order to address ourselves to the problem (2) we must know the sequential process during which the jet wave is growing up to establish the steady periodic oscillation. The problem (3), which is subtle and difficult, will be addressed after solving the problems (1) and (2) in the future.
A simple theory formulated by Fletcher[1] should be modified to give a closer fit to the visualized result of the jet shape near the flue exit. This modified theory shows the wavy behavior as displayed in Fig. 2, where the amplification factor and the spatial wavenumber (corresponding to the angular frequency divided by the phase velocity of jet wave) are assumed to be 0.22 [1/mm] and 0.25 [1/mm], respectively. The solid lines show the wave shapes calculated at the interval of 1/8 of the period T. As the time proceeds, the jet waves in Fig. 2 deflect from the inside to the outside of the pipe. We may see that a wave crest is gradually growing up and propagating toward the edge. This propagation velocity is measured as about 0.4 times the jet velocity at the flue.[2] If such propagation velocity is applied, the spatial wavenumber takes a value between 0.15 and 0.30 [1/mm] in most cases.
The broken line in Fig. 2 corresponds to the envelope of the jet waves. This envelope can be determined from the visualized jet shapes and also mathematically defined from the modified theory above. The mathematical form of the envelope is given as the hyperbolic cosine function of (amplification factor) x (distance from the flue).[3] Of course, the actual amplitude of the jet wave (and therefore the envelope) depends on the magnitude of the acoustic particle displacement at the mouth opening. So, let us fix this magnitude to be 1 mm at first and compare the visualized envelope shape with theoretical ones drawn for various values of amplification factor beforehand. We can check the fit between them by shifting the visualized shape up and down. The magnitude of this shift gives an estimation of the acoustic particle displacement.
As the result the visualized shape was approximated well by the theoretical shape in a limited scope of the present experiment. The organ pipe used is 120.1 cm in pipe length, 49 mm in pipe side, 15.8 mm in cutup (flue-to-edge) distance, and 2.2 mm in flue thickness. The sounding frequencies were about 134, 267, and 406 Hz in the first, second, and third modes, respectively. The estimated values of the amplication factor and the particle displacement were (0.22 [1/mm], 1.2 [mm]), (0.20, 1.0), and (0.24, 0.85) in the first, second, and third mode excitation for the blowing jet velocity of 11, 17, and 32 m/s, respectively. For the verification of this result the measurement of the acoustic particle velocity should be required. Such measurement using a hot-wire anemometer is on the way in the laboratory.
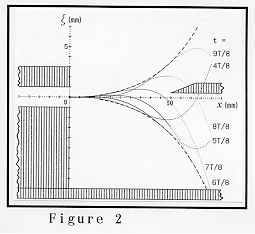
The amplification factor of the spatially growing jet seems to be almost constant (0.20 to 0.24). However, the acoustic particle displacement (or velocity) at the mouth can be responsible for the sounding amplitude when the blowing pressure is varied. The near constancy of the amplification factor suggests that the instability peculiar to the jet flow is working around its limiting (or the most efficient) condition with a good response to the acoustic flow at the mouth opening.
Figure 3 is a waveform of the acoustic pressure measured in the pipe when the blowing pressure is suddenly applied and reaches to a nearly steady value of 7 mm in water gauge (corresponding to 11 m/s of the jet velocity). Since the application of pressure was relatively slow, building up of the acoustic pressure is delayed more than the usual cases (the time origin is taken as the instance of pressure application). However, this delay is not only due to a slow pressure application, but also due to small oscillations between about 250 and 400 ms. Frequency analysis of this duration indicates that the oscillations are almost sustained by two components: (1) a 273-Hz component higher than the fundamental of 134 Hz; (2) a lower frequency component asending from about 80 Hz to 95 Hz along to the second mode resonance of the pipe, and a lower frequency between 80 and 95 Hz possibly corresponds to vortex motion at the mouth opening, which seems to have some relation with the edge tone. A mode locking required for higher harmonics to make a musical tone in the steady state is not established until some trigger finishes this edge-tone-related oscillation and the jet deflection grows up more.
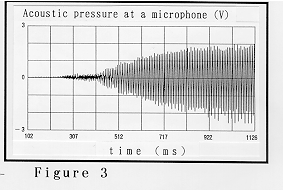
Figure 4 displays ab initio transfiguration of the jet which produces the waveform shown in Fig. 3. Interestingly enough, the jet has two crests along it when small oscillations are kept (see frames #0410 to #0509). This two-crest mode may be sustained by a "simultaneous double feedback": The lowest dominant frequency (80-95 Hz) is determined by the overall separation-reformation process of the two-crest jet; the higher dominant frequency (273 Hz) is simultaneously excited by the rear-crest jet after the two-crest jet is separated and a stagnant vorticity is formed at the mouth. According to the visualized result of Fig. 4, "some trigger" above seems to be given by straight impingement of the jet on the edge (see #0739). Immediately after this trigger is given, the two-crest mode is transfigured into the one-crest mode (#0744), which yields the mode locking between harmonics.
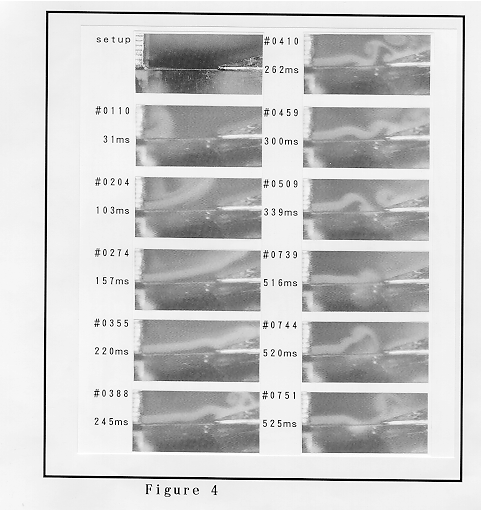
Although the results shown in this paper were obtained from a slightly unusual situation (a long cutup of 15.8 mm and a low blowing pressure for the first mode excitation), they suggested an underlying physics, particularly on the initial transient. A more intensive study of the vortex formed between the flue and edge in the two-crest mode would lead to deeper understanding of the generation of the organ pipe tone splitting off from the edge tone.
Footnotes
1. N.H. Fletcher and T.D. Rossing, The Physics of Musical Instruments (Springer-Verlag, New York, 1991) p. 432.
2. J.W. Coltman, "Sounding mechanism of the flute and organ pipe," J. Acoust. Soc. Am. 44, 983-992 (1968). H.S. Fletcher and S. Thwaites, "Wave propagation on an acoustically perturbed jet," Acustica 42, 323-334 (1979).
3. The modified theory gives the mathematical expression of the envelope as (v/[omega dot]) [cosh([mu]x) - 1], where v denotes the acoustic particle velocity at the mouth opening, (omega dot) the angular frequency, (mu) the amplification factor, and x the distance from the flue exit.