Acoustical Society of America
133rd Meeting Lay Language Papers

Star in a Jar: A New Model for Single-Bubble Sonoluminescence

William C. Moss - wmoss@llnl.gov
Douglas B. Clarke
David A. Young
(as told to Michele S. Moss)
Lawrence Livermore National Laboratory
P. O. Box 808
Livermore, CA 94550

Popular version of Science 276, 1398 (1997) and Paper 2aPA10
Presented Tuesday morning, June 17, 1997
133rd ASA Meeting, State College, PA
Embargoed until June 17, 1997

Sonoluminescence (SL) is a mysterious process in which sound waves aimed at a container of water nucleate, grow, and collapse many gas-filled bubbles to create ultrashort light flashes representing a trillionfold focusing of the initial sound energy. SL was discovered in 1933, but the phenomenon could not be studied in detail until 1990, when Felipe Gaitan [1] at the National Center for Physical Acoustics in Mississippi successfully obtained SL from a single air bubble. We have developed a new theoretical model for single bubble sonoluminescence (SBSL) that for the first time is consistent with experimental results and makes predictions about the sensitivity of SBSL to various parameters. For example, this model provides an explanation for the ultrashort light flashes, predicts that the duration and spectrum of the light flashes may be very sensitive to the maximum radius of the bubble, and supports a theoretical prediction by Lohse [2] that the gas inside a sonoluminescing air bubble may be comprised solely of argon.

In single bubble sonoluminescence, sound waves levitate and trap a single micron-sized gas-filled bubble while forcing it to undergo SL repetitively. A bubble of air undergoing SL appears electric blue in color to the naked eye. Using Gaitan's methods, experimental measurements at UCLA [3] showed that single-bubble sonoluminescence from an air bubble produces light flashes that are synchronized with the periodically expanding and compressing sound field. In addition, each flash had a measured duration of less than 50 trillionths of a second, or 50 picoseconds (ps). In addition, the light flashes produce a spectrum of colors consistent with the idea that the sonoluminescing bubble has a temperature of at least 23000 Kelvins.

These results created a scientific stampede in which experimentalists obtained more data and theorists tried to explain the data, especially the mechanisms underlying the ultrashort flashes and high temperatures of the bubble. Scientists proposed exotic mechanisms such as quantum vacuum fluctuations, fractoluminescence, and charged liquid jet collisions. Nevertheless, what remains perhaps the most popular hypothesis for sonoluminescence was first made back in 1960 by Peter Jarman of Imperial College in London. Jarman proposed that the collapsing bubble generates an imploding shock wave that compresses and heats the gas in the bubble.

Although previous theoretical work by us and others suggested that Jarman's explanation may be valid, no theoretical model of SBSL prior to our current work has explained enough of the experimental SBSL data in sufficient detail to establish any model's credibility, nor has any model made predictions that can be tested.

Our model has two basic assumptions. The first assumption is that as the bubble collapses, the gas inside is compressed and heated. This is analogous to the heat that is generated in the housing of a foot pump when it is used to fill a tire. The second assumption is that the hot gas emits light.

We performed fluid dynamics simulations of the growth and collapse of a gas-filled bubble and the liquid surrounding it [4]. We used the computer "code" LASNEX, which contains all of the physics in our model. LASNEX is also the same code used for calculations of a form of thermonuclear fusion known as inertial confinement fusion, in which lasers compress a pellet to such high temperatures and densities that fusion reactions occur between atoms in the pellet.

Our calculations show that during the collapse of the bubble, a shock wave is generated that compresses and heats the contents of the bubble. More heating occurs at the center of the bubble than at its boundary because the shock wave's strength increases as it approaches the bubble's center. In the hotter regions, the atoms and/or molecules which make up the gas trapped inside the bubble begin to break down or "ionize" into negatively charged electrons and positively charged ions. What results is a "plasma," or collection of charged particles that is partially ionized (approximately only 1 free electron per ion). The hot gas emits light by a rapid (on the order of quadrillionths of a second) cascade of energy from the ions in the plasma, to the electrons, to the photons that make up the light pulses.

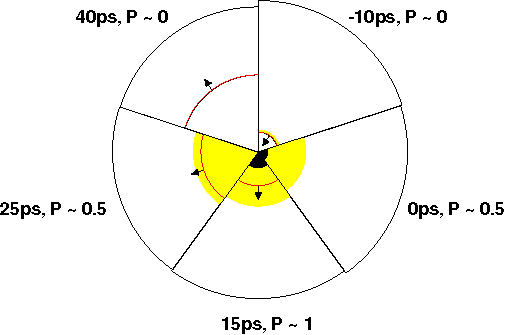
Figure 1. The final 50 ps of the calculated collapse of an argon bubble. The bubble radius (outermost curve), shock wave location (inner curve), and emitting regions [optically thin (shaded), and optically thick (solid)] are shown. P is the relative emitted power (energy per unit time) of light in the visible part of the spectrum.

The figure shows our calculated results for a collapsing argon bubble. Five snapshots of the final 50 ps of the collapse are shown, during which the radius of the bubble decreases from 0.45 to 0.43 microns. Time is referenced to the instant when the shock wave reaches the center of the bubble.

At -10 ps, the shock wave (solid curve) is near the center of the bubble and light begins to be emitted (lightly shaded region) just behind the shock wave. At 0 ps, the shock reaches the center of the bubble. At this point, the power (energy per unit time) that is emitted in the visible spectrum is one-half its eventual peak value.

The emitting regions of the bubble are very much like those in a miniature star: Visible light from the sun appears yellow, which is indicative of a temperature of approximately 6000K. However, the center of the sun is much hotter, nearly 10⁷ K.

This temperature can't be "seen," because the light that is emitted from the deeper regions is absorbed before it reaches the surface. This deeper absorbing region is described as being "optically thick." The solid black region in the figure shows where the bubble is optically thick. Only the light emission from the "halo" (lightly shaded region) and from the surface of the optically thick region can be seen. At 15 ps, the shock has reflected from the center of the bubble and is moving outward, but the gas outside the shock is still moving towards that bubble's center, compressing, and heating. Consequently, the emitting halo is slightly larger and the emitted visible optical power is at its peak value.

At 25 ps, the light emitting halo is even larger, but the bubble has cooled, so that the emitted visible optical power has decreased to one-half its peak value. At 40 ps, the bubble is too cool to emit light. The bubble temperature decreases for two reasons. First, the gas behind the outgoing shock wave expands and cools. Second, electrons carry away some of the heat that was created during the compression of the bubble. By comparing the times at which one-half peak power occurs, a 25 ps pulse width can be deduced from the figure, which is consistent with the experimentally measured value.

Our model agrees with many experimental results: (i) the durations of the light flashes and the spectra that they produce are very sensitive to the maximum bubble radius; (ii) the spectrum of the emitted light is described by the radiative properties of the hot gas, especially the radiation from decelerating electrons; (iii) the intensity of the emitted light from nitrogen SBSL is approximately 1/25 of that from air SBSL; and (iv) the spectrum of argon SBSL is nearly identical to the measured spectrum of air SBSL, which suggests that a sonoluminescing air bubble is actually an argon bubble undergoing SL [2], and may also explain why SBSL in noble gases (such as argon) is more intense than in diatomic gases (such as the nitrogen or oxygen that exists in our atmosphere). Our model suggests that the mechanisms that are responsible for the ultrashort (picosecond) duration of SBSL are the electrons rapidly carrying away the energy from the bubble and the very strong temperature dependence of the emission properties of the compressed gas. Our model predicts that after the main flash there cannot be an "afterglow" emitted by the expanding hot bubble.

The physics of matter under SL conditions is not yet understood completely. Our results suggest that our basic theoretical and computational strategy is valid, and that semiquantitative predictions are possible. For example, if the collapse of the bubble can be enhanced, thereby raising the bubble temperature even higher, then it may be possible to obtain a small amount of thermonuclear fusion from a micron-sized sonoluminescing bubble filled with heavy isotopes of hydrogen (deuterium or tritium). Although it remains to be confirmed experimentally that shock waves or plasmas are present in a bubble undergoing SL, no other model of which we are aware has been able to explain such a broad array of experimental data.

This work was performed under the auspices of the U. S. Department of Energy by Lawrence Livermore National Laboratory under Contract No. W-7405-Eng-48.

References

[1] D. F. Gaitan et al., J. Acoust. Soc. Am. 91, 3166 (1992).

[2] D. Lohse et al., Phys. Rev. Lett. 78, 1359 (1997).

[3] B. P. Barber and S. J. Putterman, Nature 352, 318 (1991).

[4] W. C. Moss, D. B. Clarke, and D. A. Young, Science 276, 1398 (1997).