Acoustical Society of America
136th Meeting Lay Language Papers

MUSICAL SCALES IN XOOMIJ

Contact Information During ASA Meeting:
Contacting by E-mail is preferred.
kakita@mattolab.kanazawa-it.ac.jp (regularly checked during meeting)
The author is staying at Norfolk Waterside Marriott Hotel /Tel.: 757-627-4200 or 800-831-4004/Fax: 757-628-6452

Popular version of paper 2pMU8
Presented Tuesday Afternoon, October 13, 1998
136th ASA Meeting, Norfolk, VA

Summary

What is Xoomij?

Exhibit 1 demonstrates an example of Xoomij singing, for those who are not familiar with the sound. The sound is taken from a music CD (1).

As you can hear, a high tone changes its pitch to play a tune, while at the same time, there is an accompanying low stable tone. The frequency of the low tone is about 100-200 Hz, and the frequency of the high tone is about1000-2000Hz.

Now, I will compare the spectral structures of the vowel and the Xoomij sound.

Exhibit 2 shows the frequency components of the vowel /a/, and Exhibit 3 shows the model representation of the frequency components of Xoomij. Both were calculated by a speech synthesis software. The abscissa is frequency, and the coordinate is the amplitude in dB.

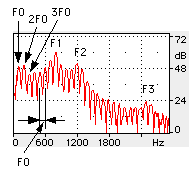
Exhibit 2 Spectral characteristics of vowel /a/. F indicates formant. F0=120Hz. For simplicity, this vowel is synthesized by a speech synthesis software.

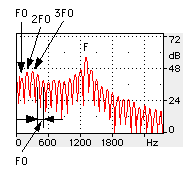
Exhibit 3 Spectral characteristics of a Xoomij sound calculated by the single-formant (band-pass filter) model. F indicates formant.

The leftmost sharp peak indicates the voice pitch, or the fundamental frequency, F0. The other peaks are the harmonics. The harmonics are defined as F0 multiplied by an integer, yielding 2F0, 3F0, and so on. The harmonics are evenly spaced in the spectrum, and consequently any consecutive pair of harmonics are separated by the value of F0.

The three dull peaks labeled F1, F2, F3, in Exhibit 2, are called formants. The combination of formants determines the kind of vowel. Each formant represents a resonance caused by a cavity in the speech organ. In speech science, the frequency characteristics of a formant is approximated by an audio band-pass filter. Since a single high tone plays the tune in Xoomij, it is natural, as a first approximation, to use a single band-pass filter to demonstrate the Xoomij sound.
As I will explain later, the fact that the frequency components of the voice are evenly spaced has a crucial influence on the construction of the Xoomij musical scale.

To check if the single-formant (or single-filter) model works, an example of synthetic Xoomij sound was produced using a speech synthesis software. (Exhibit 4b) The original sample shown in Exhibit 4a, performed by a human, is the same as that shown in Exhibit 1.

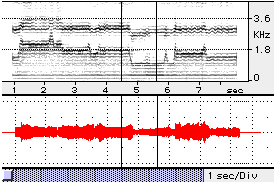
Exhibit 4a Real Xoomij tune (The same sound example as in Exhibit 1) sound: xoomij real

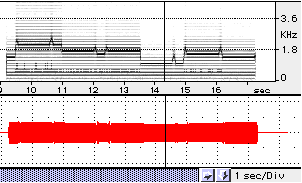
Exhibit 4b Synthesized Xoomij tune sound: xoomij synthesized

Based on a single-formant model, an example of Xoomij tune was synthesized. Exhibit 4b shows its sound spectrogram.

Exhibit 4a shows the sound spectrogram of the original Xoomij tune, which was performed by a human.

What I want to demonstrate here is that the single-format model is adequate for simulating Xoomij sounds.

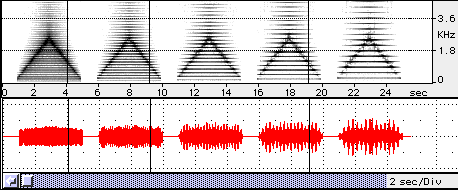
Exhibit 5 shows the sound spectrograms of five series of synthesized Xoomij sounds. I would like to show how the difference in the F0 value affects our perception of the Xoomij musical scale.

The F0 values are, from left to right, 100, 150, 200, 250, and 300 Hz. In each series of sounds, the center frequency of the band-pass filter is linearly increased from 300 Hz to 3000 Hz, then linearly decreased to 300Hz.

The higher the F0, the greater the interval of the two consecutive notes, and as a result, we perceive different musical scales.

There are two factors which influence the musical scale in Xoomij, one is the linear nature of harmonics of the voice, and the other is the selection of the harmonic with which to start the musical scale. The harmonic frequency components of voice are equally spaced in linear frequency. In contrast, musical interval is equally spaced in logarithmic frequency. In music, generally, the scale is determined by the frequency of each constituent note relative to the base note, and so the absolute frequency value does not matter.

Now, in Xoomij, too, the scale is determined relatively. However, since the consituent note must be selected from the harmonics of voice pitch, the musical scale in Xoomij is determined by the harmonic that the scale starts with.

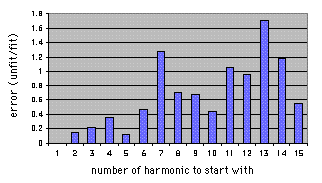
Calculations were performed to see what musical scales would be realized when the scale started with each of the 1st to 30th harmonics of voice.

Goodness of fit was obtained by examining if the n-th voice harmonic fits a musical note within the error range of plus/minus a quarter semitone. The frequency range examined was from -1 to +2 octave from a practical point of view.

Exhibit 6 Unfit/fit errors when the scale started with the n-th harmonic

In Exhibit 6, the abscissa indicates the number of harmonic with which the scale starts, and the ordinate indicates the unfit/fit error rate.

As a result, the unfit/fit error rate was the lowest when the scale started with the 5th harmonic. So, thoeoretically this can be said to be the most appropriate scale in Xoomij.

The scale starting with the 5th harmonic is shown in this figure. The scale starting with the 5th harmonic is " do #re #fa #so #la do2 --- #re2 --- #fa2 so2 #so2 la2 #la2 si2 do3" when the base is selected as "do".

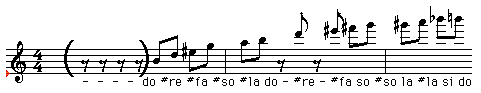
Exhibit 7 Scale starting with the 5th harmonic. 1-4th harmonic are in ( ) and are not shown. The symbol " ", also shown as "-" in the text, means that the harmonic does not fit the semitone scale. The notes are based on F0 = 200 Hz.

Although the scale starting with the 5th harmonic is theoretically the most appropriate, the examination of the sound data of actual Xoomij performances indicates that the most frequently used scale is the scale starting with the 4th harmonic.

The scale starting with the 4th harmonic is shown in this figure. The scale starting with the 4th harmonic is "do mi so --- do2 re2 mi2 --- so2 --- --- si2 do3"

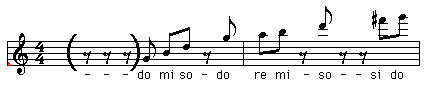
Exhibit 8 Scale starting with the 4th harmonic. 1-3rd harmonic are in ( ) and are not shown. The symbol " ", also shown as "-" in the text, means that the harmonic does not fit the semitone scale. The notes are based on F0 = 200 Hz.

Why performers prefer the scale starting with the 4th harmonic is left for future studies. One possible reason is that the sounds in the high frequency region in the scale starting with the 5th harmonic is difficult to produce, because it needs a very fine adjustment of the size of a small cavity.

*After this meeting the author will start his sabbatical stay at Ohio State Univiersity till March 31, 1999.
Address: c/o Professor Osamu Fujimura, Department of Speech and Hearing Science, Ohio State University, Pressey Hall Room 103, 1070 Carmack Rd., Columbus OH 43210-1002
E-mail: kakita@mattolab.kanazawa-it.ac.jp