Helmut Fleischer - helmut.fleischer@unibw-muenchen.de
Institute of Mechanics
Faculty of Aerospace Engineering
University of the Federal Armed Forces
D-85577 Neubiberg, Germany
Popular version of paper 5aMUb6
Presented Friday morning, March 19, 1999
ASA/EAA/DAGA '99 Meeting, Berlin, Germany
Why is the "sustain" generally better for an electric guitar or bass than for an acoustic one?
The musical signal of an electric guitar or bass originates from string vibrations. In contrast to comparable acoustic instruments, the electric ones do not radiate the sound themselves. Since there is no need to transfer energy from the strings via the bridge, the body may be made from solid material. The string supports are relatively immobile and the strings vibrations, consequently, do not decay as rapidly as for a self-radiating instrument. That means that the "sustain", which is considered as a quality attribute, generally lasts longer for an electric guitar or bass than for acoustic models.
What are "dead spots"?
However, this long decay is not observed for each fret at which the player fingers a string. There are particular locations on the fingerboard where the sustain of a string is considerably shorter than for adjacent frets. This irregularity is well-known among players of electric basses and guitars; they call it a "dead spot". An electric guitar of the well-known Stratocaster type is chosen as an example to illustrate the effect and its diagnosis.
How can dead spots be quantified?
The sustain is quantified by the decay time (in our investigation: defined by a 30 dB level difference) of the total signal at the output socket of the neck pick-up. In the normal case, the decay time decreases steadily with increasing fret number. As an exception to this rule, the decay proves as uncommonly short e.g. at the 4th fret of the D string of the Stratocaster indicating a dead spot. At the same string the contrary ("live spot") holds for the 11th fret. An additional study has revealed that the decay of the total signal is ruled by the fundamental tone of the complex string signal.
What causes dead spots?
Resonances of the instrument are supposed to cause dead spots. The vibrations were measured using a Laser Doppler Vibrometer. Since the boundary conditions of an object influence the vibrations to a high extent, special care was taken to perform the measurements in a normal playing position ("in situ"; cf. Fig. 1). The guitar was excited by random noise via mini-shaker at the rear of the neck. Several resonances were found. An example for 430 Hz is given in Fig. 1. Obviously, at particular frequencies the guitar does not at all respond rigid but exhibits pronounced resonances.
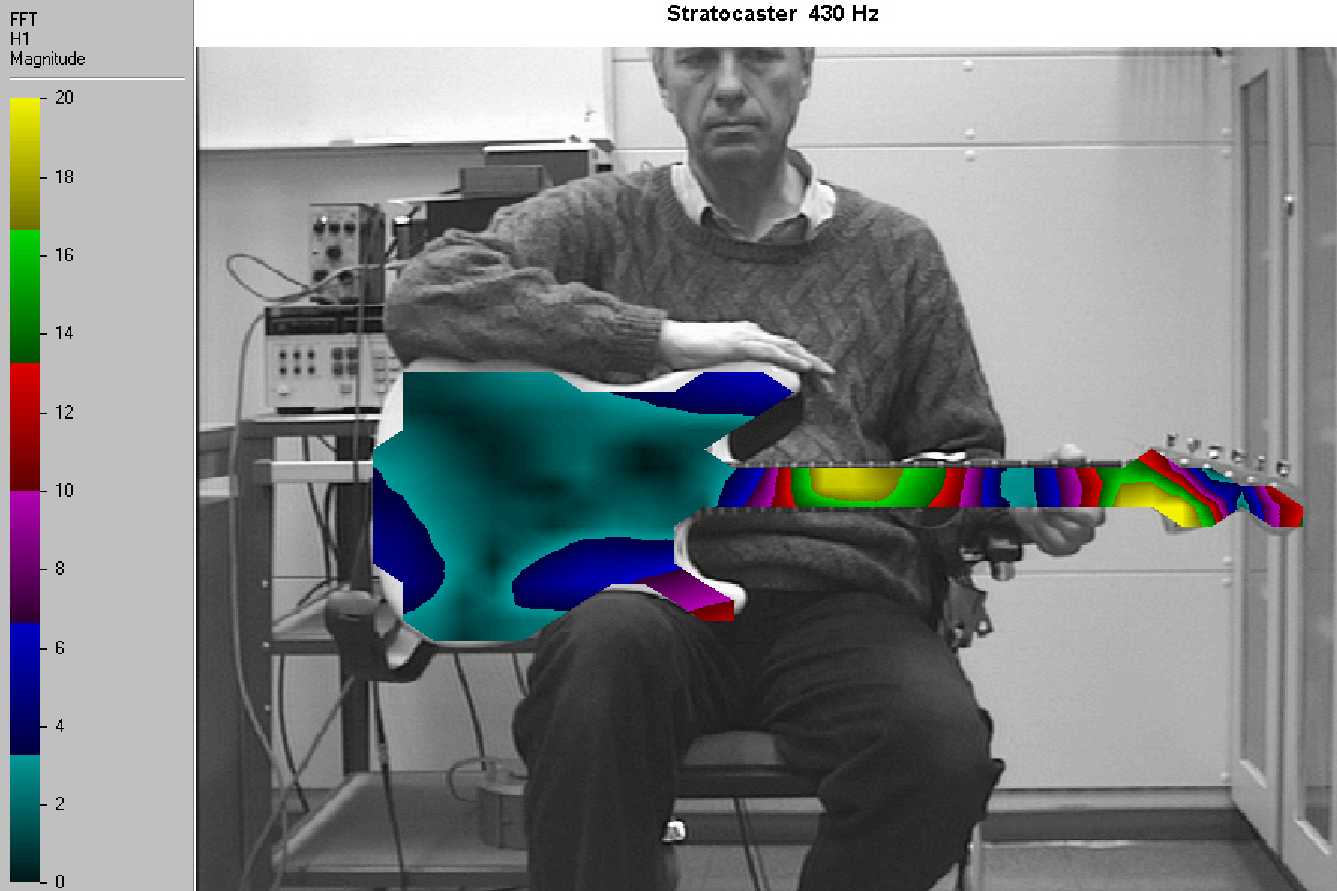
Fig. 1 In-situ measurement of body vibrations by means of a Scanning Vibrometer. A vibration pattern of an out-of-plane resonance at 430 Hz is given.
Which of both, the bridge-end or the neck-end support of a string, is more mobile?
Experiments indicate that, in the normal case and in obvious contrast to an acoustic instrument, the bridge of a solid-body electric guitar or bass is much less mobile than the neck. The string may induce body vibrations via the neck rather than via the bridge. Energy is transferred to the instrument and gets lost for the string vibration. The "vibration willingness" of the neck is the cause for additional damping of the strings, i.e. for dead spots. Former studies have revealed that the motion of the instrument perpendicular to the fingerboard dominates this effect.
Under which conditions may a string excite a neck resonance?
In order to induce a vibration of the neck by an excitation from the string two requirements must be fulfilled:
In that sense the body vibrations are not easily interpreted in terms of an excitation by the strings.
Which measuring parameter suits to characterize energy losses at the string supports?
The point admittance (velocity/force), measured at the neck-end of the strings, promises to be a more direct parameter. Its real part, the conductance, characterizes the transfer of energy via a string support. The conductance was measured in situ with a subject holding the instrument in playing position. The force and velocity were simultaneously picked up by an impedance head which was mounted on a shaker and perpendicularly pressed against the fingerboard. The signals were analyzed by a dual-channel FFT analyzer. The diagram in Fig. 2 shows a condensed 3-D representation of the normalized neck conductance. The curves were measured at the positions of the nut and first 19 frets as indicated by the numbers and combined to one diagram typical for each guitar or bass. A conductance "landscape" is created in which the "mountains" reflect the resonances (Fig. 1) of the instrument. The higher the conductance, the more energy will the string loose if fingered at the corresponding fret and vibrating with the corresponding frequency.
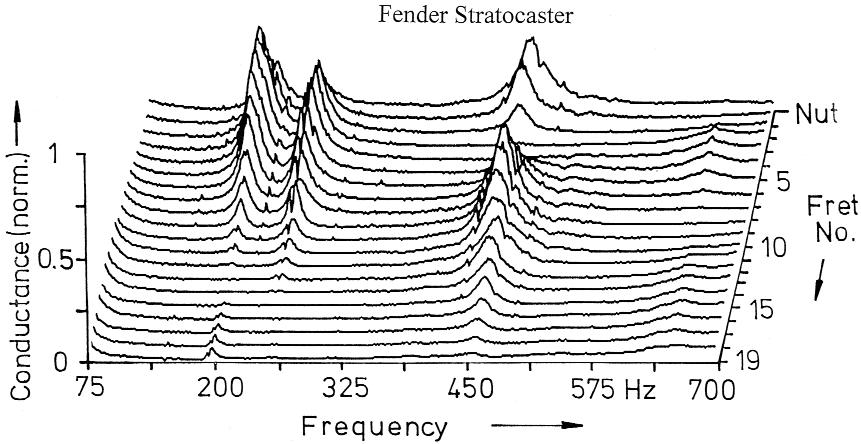
Fig. 2 - Conductance as a function of frequency measured along the fingerboard between the two mid strings from the nut to 19th fret.
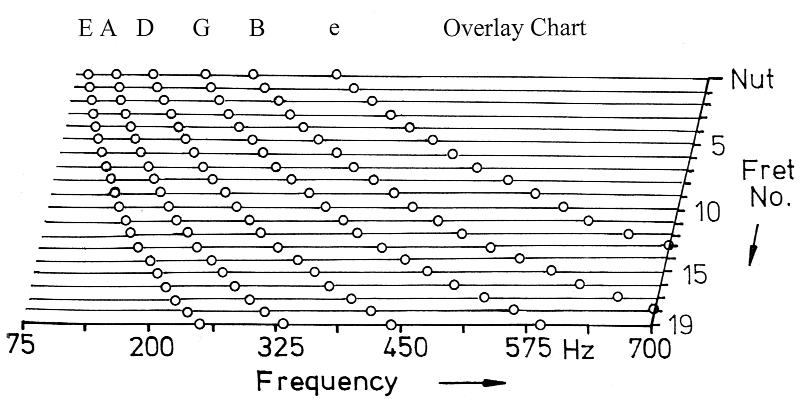
Fig. 3 - Overlay chart featuring the fundamental frequencies of all string-fret combinations.
How to interpret the conductance "landscape"?
Since a high conductance corresponds to high damping of the string at the corresponding location and frequency, the peaks serve as indicators for possible dead spots. Only distinct location-frequency combinations are used on a guitar. They are marked in the overlay chart of Fig. 3, which is intended to interpret the conductance landscape. The circles indicate the fundamental frequencies versus the fret positions (open and fingered up to the 19th fret) for all six strings in standard tuning. For basses a modified chart including the four to six strings is used. The magnitude of the conductance (Fig. 2) has to be checked for each string-fret combination. Coincidence with a high value (mountain) suggests a dead spot, with an extremely low value (valley or plane) a life spot. Comparisons between different experimental data for several guitars and basses confirm these relations and verify the neck conductance as a key parameter for diagnosing dead spots.
What, in summary, is new?
At the first glance, an electric guitar or bass looks rather rigid. At the second glance, however, it proves as very flexible at particular frequences. A dead spot, defined by an abnormally fast decay of the fundamental tone, is caused by damping due to energy transfer from the string to the instrument body. For a well-balanced instrument the bridge proves as practically immobile, while the neck is flexible and exhibits resonances. Under certain circumstances, the string may excite a neck resonance with the result that the string vibration is additionally damped. The mechanical conductance is a suitable indicator of the frequency-selective damping of the string supports. An in-situ measuring approach is suggested to ascertain the out-of-plane conductance on the neck. The combination of the curves as obtained at the nut and frets creates some kind of a landscape which represents a "fingerprint" of a guitar with respect to dead spots. An overlay chart based on the fundamental frequencies makes its evaluation easier as the higher the conductance for a string-fret combination is the more probable it is to find a dead spot. Thus, the fingerboard conductance of an electric guitar or bass can be simply measured and promises to be a key parameter for diagnosing and avoiding dead spots.