Eric M. Kramer,
ekramer@simons-rock.edu
Simon's Rock College of Bard
Great Barrington, MA 01230
Popular Version of Paper
4pPa2
Presented Friday Morning, June 2
139th ASA Meeting, Atlanta, GA
Why are the packaging materials for candy, cereal, and many other household items so noisy? The answer seems to be the creases.
You can check this for yourself. Start with a thin sheet of packaging material like cellophane or Mylar (a portion of the transparent wrapper from a large pack of cookies works well). If you can find a piece with few creases, then small deformations of the material should produce little or no noise. Next, crumple the sheet into a ball and smooth it back out. You should find that a network of sharp creases forms during the compression, and that the sheet will no longer lie flat. Repeat this procedure a few times, to generate additional creases. Now you should find that even a small deformation of the material will produce the familiar rustling sound of a crumpled candy wrapper.
Most of the research reported in this talk was conducted in collaboration with Alexander Lobkovsky (now at NIST in Gaithersburg, MD) while at the University of Chicago. We made high-resolution digital recordings (48 kHz) of the sound produced during the deformation of heavily creased sheets of Mylar. The sheets were 10 cm x 10 cm, with thicknesses ranging from .001 to .01 inches. Prior to recording, the sheets were crushed by hand 30-40 times in succession, with the expectation that this would give a reproducibly rough state.
Figure 1 shows a plot of sound amplitude vs time for a Mylar sheet .003 inches thick (click here to listen to an AIFF audio file). The sound is clearly resolved into clicks -- discrete pulses of sound with a typical duration less than 10 ms. We found that the sound emitted by crumpled Mylar sheets of all thicknesses is qualitatively similar. Thicker sheets produced fewer clicks and were somewhat louder, but the statistical features of the sound remain the same.
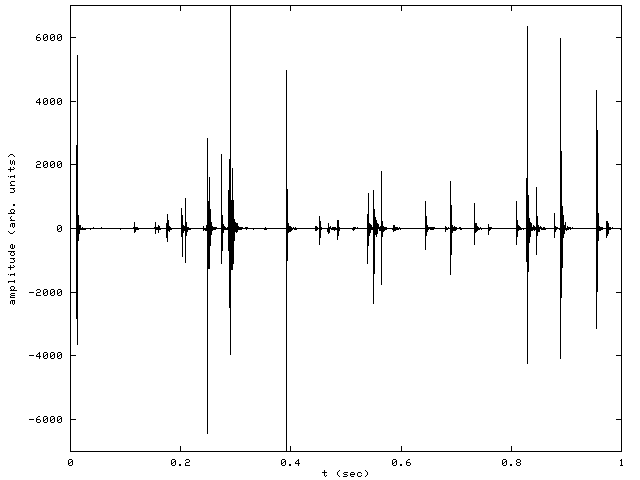
FIG.1. Amplitude vs. time for 1 second of sound data from a sheet 3 mil thick.
Another remarkable feature is the range of energy scales represented in Figure 1. The energy of a sound wave is proportional to the square of the amplitude, so the energy range of clicks from the smallest to the largest is at least a factor of one million.
The origin of the sound is related to an unusual property of heavily creased sheets. An uncreased sheet in the absence of external forces will adopt a flat configuration. By contrast, creased sheets do not seem to have a unique preference. Manipulating a sheet by hand, we can find many distinct stable configurations. Fig. 2 illustrates this observation.



FIG. 2. Three stable conformations of a heavily creased Mylar sheet. Casual examination suggests that a single sheet may have hundreds of stable states. The dimensions of the sheet are 8 cm x 9 cm x 0.0005 in.
Physicists understand this behavior by analogy with a stone rolling on a hilly landscape (technically, this landscape is the elastic potential energy as a function of sheet conformation). The landscape representing an uncreased sheet is smoothly sloping and has a single valley. A stone placed anywhere in the landscape will eventually roll into the valley, just as an uncreased sheet will settle into the flat configuration in the absence of external forces. Conversely, the landscape representing the crumpled sheet is rough, with many ridges and valleys. Each valley corresponds to a distinct stable configuration for the rough sheet.
This suggests an intuitively simple picture for the mechanism of sound generation in a crumpled sheet. Small deformations put energy into the sheet, which is stored as elastic potential energy. Eventually, enough energy is stored that the sheet "snaps through" to a new configuration. In the landscape analogy, this corresponds to pushing the stone up the hill until it reaches the top of a ridge. The stone then rolls down into the adjacent valley. Observation of the sheet during deformation confirms that each click is emitted during a sudden change in conformation.
This also explains a fact familiar to anyone troubled by their inability to quietly unwrap candy in a movie theater. You can slow down the frequency of the clicks by decreasing the rate at which you unwrap the candy, but you have no control over click loudness. In the landscape analogy, you can control the rate at which you push a stone up a hill, but when it rolls down into the next valley, you've lost control.