The Crack-of-the-Bat: The Acoustics of the Bat Hitting the Ball

Robert Kemp Adair- adair@hepmail.physics.yale.edu
Yale University
203-432-3370

Popular version of paper 5pAA1
Presented Friday afternoon, June 8, 2001
141st ASA Meeting, Chicago, IL

When I was asked to talk at this meeting about acoustics in baseball, I objected, saying that "I knew nothing of acoustics." But my complaint was overruled as irrelevant. And perhaps the overrule was correct. While in science it is surely most important to find the answers to the questions, it is also important to frame those questions -- and I can say something about the question, "What does acoustics have to do with baseball?"

I'll answer that question first briefly by noting that sometimes the difference between the sharp acoustic crack-of-the-bat and a sullen acoustic clunk-of-the-bat can be worth a run or two.

When a baseball is hit straight at an outfielder he cannot quickly judge the angle of ascent and the distance the ball will travel. If he waits until the trajectory is well defined, he has waited too long and will not be able to reach otherwise catchable balls. If starts quickly, but misjudges the ball such that his first step is wrong (in for a long fly or back for a short fly), the turn-around time sharply reduces his range and he will again miss catchable balls. To help his judgment, the experienced outfielder listens to the sound of the wooden bat hitting the ball. If he hears a "crack" he runs out, if he hears a "clunk" he runs in.

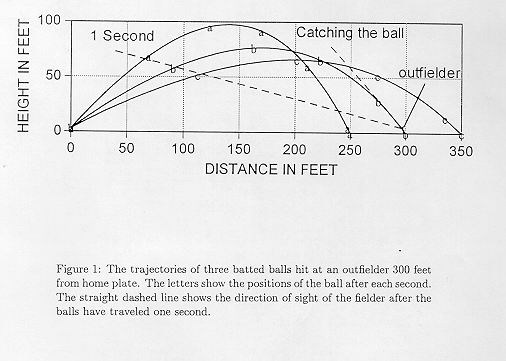
Figure 1 shows the trajectories of three balls viewed -- with consternation -- by a player 300 feet from home plate. One will land 50 feet in front of him after traveling for 5 seconds, one will drop into his glove if he stays put about 4.6 seconds after it left the bat, and the third will land 50 feet behind him 4.3 seconds after the batter hit it. For the first second, the paths of the three balls look the same to the fielder -- and the situation is only clarified a little after 2 seconds. Then for too long, his view of the rising ball gives him little to tell him whether he should run in, run out, or stay put. {At the distances of the ball from the fielder, binocular depth perception is irrelevant and the resolution of the eye is insufficient to make easy use of the different subtended size of the ball at the fovea.}

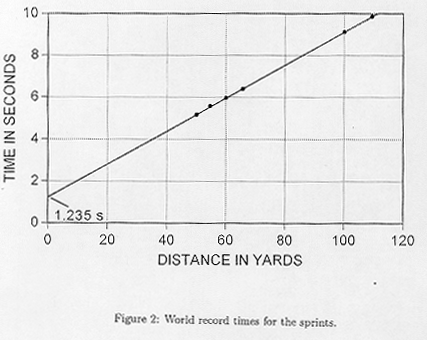
To consider the fielder's problem quantitatively, we must also ask always "can he get to the ball in time?" To respond to that query intelligently we must look into the running speeds of ball players. Figure 2 shows the 1998 world records for various sprint distances. We can summarize the results by noting that a runner takes 1.25 seconds to get started and then runs at a speed of about 38 feet per second -- all, of course, running in a predetermined direction out of starting blocks onto an especially prepared track, and wearing special suits and shoes.

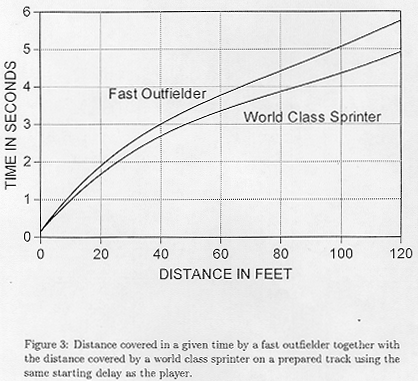
A baseball player, not running out of blocks, and -- more important -- with no pre-knowledge of what direction to go! -- surely cannot start as fast as the sprinter. I estimate that he needs an extra half-second. And running with baseball spikes on grass, in a baseball uniform, carrying a glove, and glancing his shoulder at the ball as he runs, I take 30 feet per second as the running speed of a fast outfielder going after a ball. Figure 3 shows the distance the ball player runs as a function of time using that model, together with the distance the sprinter -- in a track suit, with track shoes, etc and running 38 feet per second, would cover assuming he has the same start delay as the player.

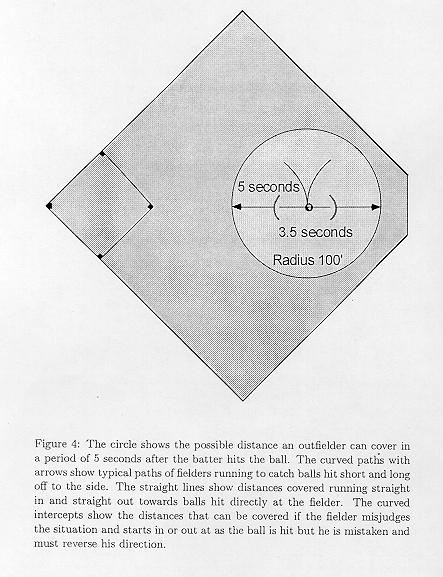
Then with this information, in Figure 4, I show a cartoon of the distance, about 100 feet, that an outfielder -- playing center field for definiteness -- can cover in 5 seconds, a typical flight time for a flyball, if he ran in a straight line and started out as he saw the batter hit the ball (not at the crack of the bat, the sound of which would take about 0.3 seconds to get to him and thus take 10 feet off of the radius of the acreage that he could cover.) The curved lines show typical actual paths traversed in catching short and long balls hit off to the side. To the 1.75 seconds starting time, I have added 0.3 seconds as the flight time necessary for the fielder to detect whether the ball was hit to his left or right. He can start immediately to his right and run in that direction for the one or more seconds that gives him enough information to see that the ball will land long or short. (He is then effectively looking at the trajectory of Figure 1 from the side as we are.) Of course, the delay in starting and the extra distance he must run reduces his range to about 85 feet in the 5 seconds after the bat hit the ball.

But the fielder is in trouble when the ball is hit at him. He can't make an informed decision to run in or out until more than 1.5 seconds have elapsed. Since, from Figure 3, we see that he can run 50 feet in 3 1/2 seconds he will not quite get to the short ball shown in Figure 1 which will fall for a single, and if the batter has hit the ball well, as the long ball in Figure 1, it will sail well over his head for a double. Balls that could have been caught easily if he had started promptly will have gone for hits.

So what can the fielder do? He can start earlier using uncertain information, but if he is wrong, if he runs in when he should have run out, or vice versa, he is dead. The extra, stop, turn around, restart, and run a few feet extra will cost him an added 2 seconds and reduce his range to about 40 feet (from Figure 3) and he will be able to catch neither the long nor short ball.

What he can do -- and does -- is sharpen his discrimination by using other clues. If the batter is half fooled and swings awkwardly, the ball is more likely to be short. And, perhaps most important, after 0.3 seconds he hears the sound of the bat hitting the ball. A one-time center fielder told me "If I heard a crack I ran out, if I heard a clunk, I ran in." The well-hit ball sounded "crack," the mis-hit ball "clunk." Where did those noises come from?

In brief, the well hit-ball is hit near vibrational nodes of the bat (and near the "sweet spot") {The baseball player's "sweet spot" is the node of the 170 Hz fundamental vibration of the bat. Balls hit at that point generate no 170 Hz vibration. The sensory system is quite sensitive to that frequency -- and quite insensitive to the frequencies of the higher harmonics.} and generates minimal energy-sapping bat vibrations. conversely, the mis-hit ball, where the impact point is far from the sweet spot region, generates large vibrational amplitudes in the bat that both take up collision energy and sing acoustically.

A typical wooden bat struck by a ball vibrates with a fundamental frequency near 170 Hz, a second harmonic of about 550 Hz, and a third harmonic of about 1100 Hz. {The vibrational spectrum was first calculated by L.Van Zandt and measured by Uwe Hansen. The energy transfer to the ball was first calculated correctly by Allan Nathan. Nathan's results were confirmed by field measurements by Tres Crisco and Michael Greenwald.} A ball-bat collision extends over about 0.5 milliseconds thus dampening the higher frequencies. The configurations are shown in Figure 5.

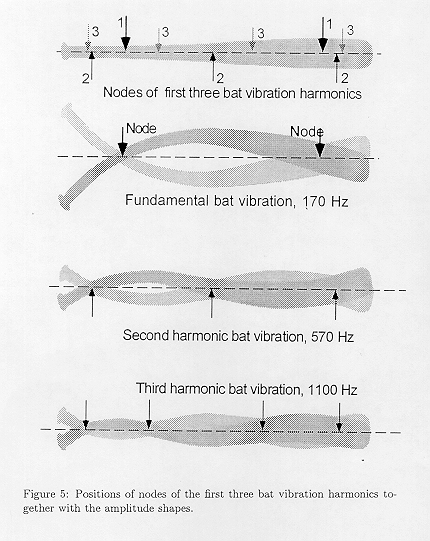
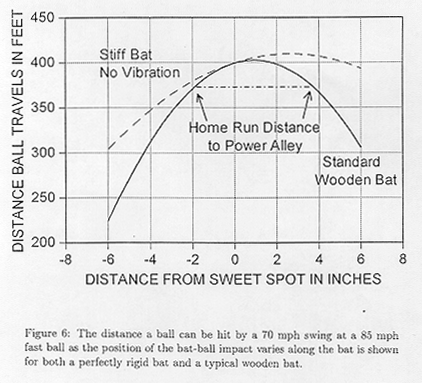
Both kinematic effects and energy transfers to the bat govern the distance a ball goes when hit by a bat. Figure 6 shows that distance as a function of the ball-bat impact point on the bat for an ideally rigid bat and for a typical real bat for a ball velocity of 85 mph and a bat velocity such that the nodee of the fundamental travels 70 mph. The effects of energy transfers to the bat vibrations are evident.

From Figure 6, we see that the ideal place to hit the ball is about one inch beyond the baseball batter's sweet spot (the node of the fundamental) and thus in a region that contains the nodes of the three primary vibrational modes. Here, the energy transfers to the vibration of the bat are minimal and the bat acts almost as a perfectly rigid bat.

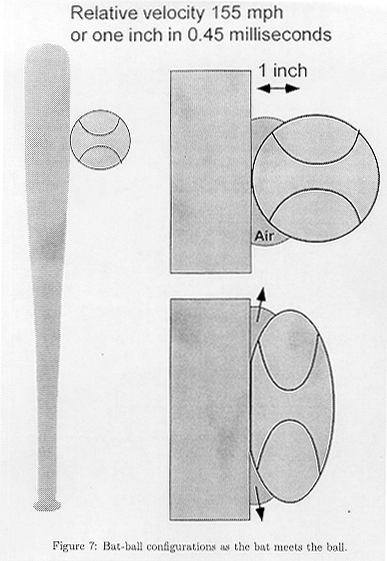
For such a bat the primary acoustic disturbance follows from the expulsion of the air from the region between the bat and the ball upon the collision. Figure 7 shows a cartoon that suggests the character of that impact. Approximately 100 cm³ of air are expelled in less than  of a second. Taking the speed of sound as roughly c = 1100 feet per second, we see that , in terms of the characteristic length  the source is localized sufficiently so that we will make no serious error in our approximations by assuming the propagation of the sound is isotropic.

From dimensional considerations, I take the acoustic energy as w = . Estimating  with the energy in an impulse with a width of about 0.5 millisecond -- or a base frequency of about 500 Hz. At the oufielder's distance of 300 feet, the energy density will be about . I identify this sound as the ''crack of the bat."

When the ball is mis-hit, the vibrational frequencies are excited. I consider that the primary modification of the crack comes from the relatively low frequency fundamental of about v = 170 Hz. We do not have good measurements of the  Q-value, but it seems that it may be about 10. Hence, the sound has a duration that is of the order of 50 milliseconds. From the energy lost to the collision, as calculated by Nathan, the amplitude of the oscillation, for a ball hit on the end of the bat or a few inches near the handle from the sweet spot, will be, typically, a centimeter with a surface velocity of about v = 10 m/s.

From Figure 5, we estimate the effective length of the source as about 0.5 meters. This is sufficiently smaller than the wavelength of about 2 meters, that we should incur no large error by assuming the sound is radiated isotropically. I then make a crude estimate of short-time radiated power density, S, at a distance of the fielder from home plate feet r = 300 feet = 90 m,