|
Lori L. Holt - lholt@andrew.cmu.edu Andrew J. Lotto - lottoa@boystown.org Popular version of paper 4pSC1
|
 |
Introduction
Consider the daunting task that lies ahead of the infant learning the sounds
of his or her native language. Each language uses a set of distinct sound categories,
or phonemes, to distinguish meanings of spoken words. Some languages use over
100 of these "sound letters" while others use only a dozen. An infant
language learner doesn't know which sounds are phonemes in their language or
even how many phonemes there are to be learned. To make matters worse, some
of the differences in speech sounds that they hear are related to differences
in phonemes (e.g. /d/ vs. /b/) but other differences are unrelated to phonemes
(e.g., whether speakers are male or female or whether they are excited or tired).
Despite these intimidating challenges, infants appear to be perceptually "tuned"
to the categories of their particular native language by the time they are 1-year-old.
How do they do it? The answer that has been gaining popularity in the last decade
is that infants (and perhaps adults learning a second language) rely, in part,
on a process called statistical learning to acquire the phonemes and other aspects
(words and syntax) of their native language. In our labs, we examine the promise
and the shortcomings of statistical learning for understanding speech perception
and other forms of complex auditory processing. The experiments involve humans
(adults) learning foreign language phonemes and completely novel sound categories
and non-human animals (e.g., birds and gerbils) learning human speech sound
categories. Here we provide a taxonomy of the different kinds of statistical
learning and the current evidence for their usefulness in learning new sound
categories.
What is statistical learning?
To understand how statistical learning would work, consider a gambling metaphor.
If you throw a fair die, the probability of any number coming up is equivalent
(1 out of 6) and the probabilities stay the same for the next roll or next 100
rolls. Likewise, if you turn up the first card on a well-shuffled deck, the
likelihood of a particular card coming up (e.g., ace of spades) is the same
for all cards (1 out of 52). If you are trying to guess what number will be
rolled or what card will be picked, no choice will be any better than any other.
But what happens if the die is fixed to come up with a six twice as often as
any other number? In that case you would be better off choosing six as a guess.
How would you discover this strategy? If you rolled the die a large number of
times and counted the number of sixes, you would see that six came up more often
than the other numbers. Likewise, if you were a card counter at a Las Vegas
casino table, you could determine the likelihood that a particular value of
card (e.g., a three) was coming up based on the cards that were already dealt.
The proposal of statistical learning is that infants are doing something akin to card counting or testing an unfair die. It suggests that the human brain keeps track of many characteristics of the sounds we hear across time and determines the probabilities or frequencies of certain characteristics. This is obviously not a conscious process and, in fact, may not even require attention to the sounds. Thus, although most of us are math-phobic, it may be that our brains are computing covariance matrices, conditional probabilities and maximum-likelihood values. The questions for researchers are: 1) How much statistical information is present in the speech that infants (and adults) hear? 2) Does the brain actually record this information across time? and 3) If so, is the information used in speech perception and language acquisition? The answers to these questions are starting to become clear. Below we present three types of statistical information and a bit of the current evidence concerning if and how humans (and other animals) use this information.
1. Distributional Information
Phonemes can be distinguished by a number of physical differences in the sounds.
For example, the sounds at the beginning of the English words "church"
and "shirt" are distinguished in part by how fast they reach full
amplitude (or loudness); "ch" has an abrupt onset, whereas "sh"
is more gradual. The actual rise times vary for each production of these sounds
but if one looks across a large number of productions there is a clear pattern.
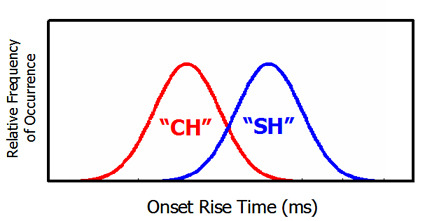
The figure below presents hypothetical distributions of the rise times; the
relative frequency of a particular value of the rise time is presented for each
heard production of these two sounds is plotted. If an infant brain was keeping
track of the probability of different values along this dimension across time
then they would see that there are quite likely two sound categories represented
here with a boundary between them at the trough in the middle. This is akin
to rolling a die over and over and keeping track of the values. If you had similar
distributions with high points at 2 and 4, you would determine that the die
was fixed for those two values.
Does the brain compute this sort of distributional information and make use of it? Recent research has suggested that infants are sensitive to distributions of speech sounds presented in a laboratory (Maye et al., 2002). After only 2.3 minutes of exposure to speech sounds from distributions like these, 6- and 8-month old infants treated the sounds as if they came from two different categories (as measured by a preferential looking time task). It appears that humans share this distributional learning ability with other animals. In an experiment we conducted with Keith Kluender and Suzi Bloedel at the University of Wisconsin (Kluender et al., 1998), European starlings (a bird species) were presented distribution of vowel sounds (the vowels in "beat" and "boot"). The birds easily learned to "label" these vowel categories by pecking a button. In addition, the birds responded most strongly to sounds that had characteristics that were most probable in the training distributions. Although this doesn't mean that your canary secretly understands everything you are saying, it does indicate that birds may keep track of which sounds were most frequent during the training like a gambler checking on the fairness of a die.
Despite these promising positive results, it should be noted that no one has demonstrated that distributional information is actually used by infant or adult humans to learn the phoneme categories for language. Additionally, recent results from our labs suggest that the actual shape of distributions have little effect on non-speech category learning and that distributional learning (when present) may be a weak effect.
2. Correlation
In addition to amplitude rise time, the sounds "sh" and "ch"
differ in overall duration in English; "sh" is usually longer than
"ch". As a result, for these sounds, short duration and abrupt rise
times tend to occur together and long durations co-occur with gradual rise times.
In other words, amplitude rise time and overall duration are correlated. One
could discover this pattern by keeping track of both values across time and
discovering the pattern. To stretch the gambling analogy, correlation would
be if a pair of dice was fixed such that they either tended to come up with
high numbers or both with low numbers.
Can humans discover correlations in complex sounds and use them to learn categories? We presented adult listeners with noises that varied in amplitude rise time and asked them to label them as "abrupt" and "gradual". Unbeknownst to the participants, the pitch of the noises was correlated with the amplitude rise time. Would the listeners pick up on this connection? After training, we tested the listeners on sounds that were halfway between abrupt and gradual, where amplitude rise time offered no help for labeling. The participants were still able to do the task using the pitch cue, demonstrating that they learned the correlation and used it. More impressively, they were completely unaware of the correlation even at the end of the experiment. They couldn't explicitly tell us which pitch (higher or lower) went with which onset (abrupt or gradual). The calculation of correlations appears to be a non-conscious obligatory process of the brain?and not just the human brain. In a separate experiment, we trained birds (this time Japanese quail) to "identify" human speech sounds (e.g., /ba/ versus /pa/) on the basis of one characteristic of the sounds by pecking to a key (Holt et al., 2001). The birds were also able to pick up on a second attribute (voice pitch) that was correlated with the first and to use it in subsequent identification tasks. Correlation appears to be a strong candidate for statistical learning. However, we must again point out that its use in phoneme learning in humans hasn't been explicitly tested.
3. Transitional Probabilities
In addition to different sets of phonemes, languages differ in the rules for
putting those phonemes into words. In English, two or three consonant sounds
can be used to begin a syllable but in Japanese a consonant must be followed
by a vowel. Even in English, there are rules about what consonants can appear
together at the beginning of a word; "str" is ok, "bps"
is not. This language-specific pattern may be learnable if one examines the
frequency of sounds appearing together across a large number of words and phrases.
These values are referred to as transitional probabilities. If one had a poorly
shuffled deck of cards, the transitional probabilities of the deal may be skewed.
If players group their hands together such that pairs and triples are placed
next to each other and the deck is not shuffled carefully the probability of
dealing two kings in a row increases.
In speech transitional probabilities can be very useful because they can help listeners determine where words begin and end. If you run across the sounds "bk" in an English speech stream, chances are that you have just hit a word or syllable boundary. Recent experiments have demonstrated that infants and adults are exquisitely sensitive to transitional probabilities in speech and non-speech sounds. Jenny Saffran and her colleagues (Saffran et al., 1996) presented 8-month-old infants with an artificial "language" made up of English syllables differing in transitional probabilities (e.g., /da/ was usually followed by ku but rarely followed by /pa/). After only 2 minutes of exposure, these infants appeared to separate strings of the syllables into word-like units at the points where the transitional probabilities were low. These results were replicated with adults and with strings of non-speech sounds. And, lest we become too proud of our human abilities, monkeys (macaques) tested with the same stimuli and design show similar results (Hauser et al., 2000)
4. Conclusions
There is quite a bit of promise for statistical learning to provide part of
the explanation for the amazing language abilities of human infants. Humans
appear especially sensitive to correlations and transitional probabilities and
perhaps to distributional information. These abilities are not special to humans
and appear to be part of our inherited toolbox for learning about the world
around us. Language learning may co-opt these abilities.
However, up to this point there is no direct evidence of the use of general statistical learning in language acquisition. Many researchers (including us) have pointed to statistical learning as an explanation without describing particular mechanisms or taking the time to assure that reliable information exists in the real-world speech environment. Ongoing research will help to determine if infants manage their way through the complexities of speech by counting cards and testing fixed dice.
5. References
Hauser, M. D., Newport, E. L., Aslin, R. N. (2000). Segmentation of the speech
stream in a non-human primate: Statistical learning in cotton-top tamarins.
Cognition, 75, 1-12.
Kluender, K.R., Lotto, A.J., Holt, L.L., & Bloedel, S.L. (1998). Role of
experience for language-specific functional mappings of vowel sounds. Journal
of the Acoustical Society of America, 104, 3568-3582.
Maye, J., Werker, J. F. & Gerken, L. (2002). Infant sensitivity to distributional
information can affect phonetic discrimination. Cognition, 82, B101-B111.
Saffran, J.R., Aslin, R.N., & Newport, E.L. (1996). Statistical learning
by 8-month old infants. Science, 274, 1926-1928
6. Acknowledgements
The authors are supported by the National Institutes of Health, the National
Science Foundation and the James S. McDonnell Foundation.