|
George Bissinger bissingerg@mail.ecu.edu |
 |
Theme: How to automate pitch-matching ten thousand drumsticks a day using
modal (vibration) analysis techniques.
Sub-theme: a drumstick is a one-dimensional violin. We want to evolve procedures
to evaluate and match violin top and back plate vibrational properties on assembly
line violin production.
OUTLINE
Pitch is a quintessentially musical term not commonly applied to drumsticks.
Yet it is considered a desirable attribute by drummers, enough to make such
matching commercially viable. For the tidy harmonic series like those from string
vibrations (where the frequencies fn = n x f1, and n is always an
integer =1,2,3…) a well-defined pitch generally comes naturally. Although
no well-defined sense of pitch is possible for drumsticks since their normal
bending modes (which produce the sound we hear) are not harmonic - or even nearly
so - there is still some sort of "pitch center" that allows one to
achieve approximate matches by ear.
Listen here for a demonstration of drumstick pitching
On the practical side, pitch matching of drumsticks is commonly done by those
unversed in any underlying psychoacoustics explanations. Choose one drumstick
from a box and then pick out any other drumstick, strike both on a hard surface
and listen for a match. This takes a few seconds for each stick match and there
is no minimum number of sticks to try. One might expect minutes on average to
make a match from a box of sticks that have not been pre-sorted by either weight
or pitch. Such rates, however, mean that using individuals to match drumsticks
by ear in manufacturing consumes far too much time to be compatible with the
many thousands of drumsticks throughput per day in normal manufacture.
There is a sensible modern solution to this problem. Understand the vibrational
behavior of the drumstick - this means understanding its dependence on density,
stiffness and shape - so well that even when it is held that one can reliably
predict the effects of holding. Our understanding of the modes of vibration
was achieved through experimental modal analysis, a technique whereby the "atoms"
of vibration - the normal modes - can be assembled into the "molecule"
of mechanical vibration that results from being set into motion.
Over 100 hickory drumsticks, in all-wood and plastic-tip models, were weighed,
examined for material defects, and vibration-analyzed to create a statistical
database. This database was then analyzed to find the range of mode frequencies
expected to set analysis frequency bands, compute frequency relationships between
modes in any one drumstick, check the effect of material defects including knots,
grain twists or kinks and on vibrational behaviors. The final conclusion was
very simple - only the frequency of the very lowest mode of vibration was necessary
to reliably pitch match drumsticks!
On the manufacturing line this knowledge was turned into a brief (~1 s) vibration
measurement after the manufacture, analyzed in few milliseconds and the drumstick
was then sorted into frequency "bins". (Weights of the drumsticks
were determined separately.) The pitch (and weight) matched drumsticks can then
be paired and sold. To date millions have been pitched using this procedure
since the manufacturer initiated the process last year.
A little side note. The pitch and weight matching also guarantees that
the drumsticks are stiffness-matched. This is due to the basic physics behind
vibrating objects where if the density(mass), stiffness and shape properties
of a material are known the vibration frequencies can be computed. So turning
this around a little, if you know the shape, density, and vibration frequencies
it is possible to get the stiffness properties.
a) frequency of vibration - the number of cycles per second
b) "damping" (our measure of how a vibrating object loses its energy - here part of the energy goes to heat (internal damping), part to sound (radiation damping) and part to whoever is holding the vibrating device (the "support fixture" damping in engineering terms). How many cycles of vibration the vibrator goes through before stopping is a measure of its damping. Damping greatly colors the perceived sound - think of a struck bell suspended by a string vs. being held with the hand.
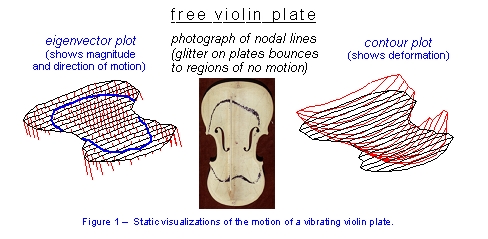
c) "shape" - this is just a profile of its motion. Simplifying the shape is commonly done by drawing a line through just the points on the object where there is no motion (nodal points) to create a nodal line. For the violin, or a violin plate each nodal line pattern for any mode is completely distinct from every other one, both mathematically and by visual inspection.
To help understand what is meant by mode shape, we will go to a two-dimensional world. Consider what happens when you scatter a powder on a plate and force the plate to vibrate. If you get the plate to vibrate in one of its normal mode shapes the powder will be bounced to the nodal regions, highlighting the regions of no motion. This technique, called Chladni patterns, has been around for centuries. Some visualizations of violin plate motions are shown below.
a) Center graphic is a photo of glitter on a wooden violin top plate that was forced to vibrate at one of its normal mode frequencies by placing it over a loudspeaker and driving the loudspeaker with a sine wave set at the normal mode frequency. The dark glitter traces the nodal lines and serves to give a shape for the motional pattern.
b) Left graphic shows motional pattern presented as a number of little bars that either go up or down at various points over the whole surface. These are the actual measured velocities at each point on the surface. Note that sometimes the bars are above and sometimes below the plate surface. If you trace a line through the places where the plate has no motion again you get a nodal line pattern.
c) Right graphic shows a greatly magnified change/deformation in the plate shape as it goes through its vibratory motions.
These three graphics illustrate some of the ways of illustrating
motion in a static presentation. The analysis software that takes the vibrations
and turns them into these graphics also has animation capability.
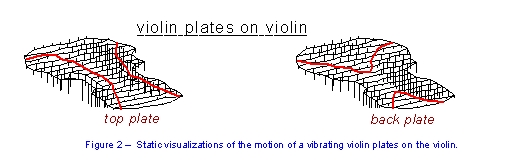
When the plates are glued to the violin ribs the vibration patterns change significantly because the edges have some constraints that do not allow them to flex freely. Modal analysis allows us to visualize these vibration changes exactly like free plates.
Finally, the whole violin vibrations for one of its normal modes is shown below. All the yellow/white (fat line) parts do NOT radiate significant sound.
