3-D Motion in Stradivari and Guarneri dG Violins
George Bissinger – bissingerg@ecu.edu Popular version of paper 2aMU1 |
|
INTRODUCTION
Old Italian violins, especially those of Antonio Stradivari and his contemporary Giuseppi Guarneri del Gesu, are a de facto standard in the classical violin world. Their status is supported by the large percentage of solo violinists currently playing these instruments. For two centuries scientists have been investigating violins to try to understand on a quantitative basis what determines a violin’s quality. To date there is no robust scientific descriptor of violin quality, and almost certainly there never will be just one quantity that could cover the wide variety of most desired violin properties. However in the last decade much entirely new vibration and sound information has become available
With the advent of the computer, especially the now ubiquitous personal computer, and the accompanying specialized vibration and acoustic analysis software, the span of technology has increased dramatically over the last two decades while costs have sunk equally dramatically. Combine this infrastructure development with the modern ubiquity of lasers and their wide-ranging applications including the scanning laser used here, and certain scientific analyses impossible to even consider three decades ago are now feasible.
This talk covers the first application to the violin of a very recent technological development, the 3-dimensional scanning laser, to measure extensional (in-plane) as well as flexural (out-of-plane) vibrations. What is so important about separating these two types of motion? The importance lies in the shell (arched) shape of the violin. If one plate of the violin was separated from the violin and then laid on a table, pushing straight down on the plate not only would tend to flatten the arch but also to extend the edges. Thus when the violin is assembled the up-down motion of the bridge feet pushes down on the plate, but also spreads the plate. The real reason why we want to know about flexural vs. extensional motions? The sound of the violin comes only from the flexural motions, the extensional motions just end up as heat!
Why not just make a violin with flat plates where extensional motions are negligible? There are a lot of ergonomic considerations that indirectly enter here - too big and it cannot be played, too small and it cannot be fingered well. Once size is set efficient vibration-sound conversion requires the longest wavelengths not to be too large relative to size. This keeps string pitches above a certain value, which in turn leads to string tension forces exceeding flat plate strengths for the nominal 3 mm top plate thickness. The obvious solution of thickening the plates for strength kills the sound. (Bassbars and soundposts do help here also.) Arching the plates was the compromise solution, re-introducing the flexural vs. extensional problem in sound production.

Figure 1 − There is very little in the top, ribs and back of the violin that could be considered straight. The shell shape of these major substructures guarantees that violin vibrations include extensional motion as well as flexural motion.
So arched it is. Here practical consequences again intrude for the solo violinist. If you play the violin in front of a full orchestra, not only are you outnumbered, but there are many instruments that are far more efficient at turning the musicians efforts into sound (think brass – trumpets, trombones, French horns, etc.). To be successful the soloist must have a loud violin that produces lots of sound in a frequency range where the orchestra usually does not, preferentially near 3 kHz where the ear is most sensitive. Why are some violins so much more successful at being heard than others? Our 3-D mobilities offer an altogether new insight into violin sound production. When the flexural/extensional motion ratio is small, the violin just raises the room temperature when played; on the other hand if it is large much more of the violinist’s work goes into sound. And if the ratio is larger than average in the top plate it helps project the sound preferentially above the violin toward the audience – directional but without beaming – so that it sounds louder, even though overall it may not be putting out any more sound than some other, less directional violin.
EXPERIMENT
A Polytec 3-Dimensional scanning laser system is comprised of three individual lasers measuring surface velocity from three different directions ( Figures 2 and 3). This allows extraction of motion components along three perpendicular directions. Such a system measured in-plane IP (extensional) and out-of-plane OP (flexural) violin corpus vibrations (in the form of mobilities = velocity/force) in the top, ribs, and back of two exemplary old Italian violins, the 1715 Titian Stradivari and the 1735 Plowden Guarneri del Gesu, plus partial scans of the Willemotte Stradivari (1734) and a Joseph Curtin (2006), back plate and top plate, resp.

Figure 2 – Setting up the tri-laser system for the 3-dimensional scans.
The violin vibrations were excited by striking a violin bridge corner with a mini-force hammer. These vibration measurements were accompanied by acoustic pressure measurements at 266 microphone positions over a sphere in an anechoic chamber on all these violins (plus a 2006 Sam Zygmuntowics violin). For violins with mobility measurements over the top, ribs, and back it was possible to compute the radiation efficiency and damping for each mode of vibration.

Figure 3 – Setting alignment points on a Stradivari to aid splicing top, back, and rib scans into a 3-dimensional model with proper orientations. The violin hangs on two thin elastics. The force hammer, whose strikes make the violin vibrate, is located above and to the right of the bridge. (Photo - East Carolina University)
The earlier 1-dimensional laser grid scans were replaced here by a mesh scan, first measuring the violin surface shape with a separate laser, then setting the mesh, and excising points in the f-hole region. These 3-D measurements require all three laser beams to strike the same points over the entire scan. Consequently, the parts (bridge, tailpiece and neck-fingerboard) above the top plate can create shadow regions over the top plate, somewhat larger than for the straight-on 1-D grid measurements. When all of the points are measured and the response curves calculated, it is a simple matter to pick out how the violin vibrates at any frequency over the 0-5 kHz range measured. A few sample screen snapshots from the animated responses for the whole violin are shown in Figure 4, with the OP and IP motions for the CBR mode shown separately. The motions are all at the same scale and give some idea of the importance of IP motions even though the bridge feet are forcing OP plate motion.
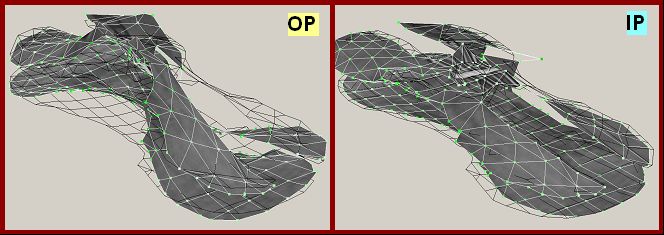
Figure 4 – Screen shots of out-of-plane (L) vs. in-plane motion (R) motion for the Plowden CBR mode (same scale). This mode has a shear-like IP motion between top and back plates.
DATA ANALYSIS
Typically data analysis after these measurements starts with a composite “spaghetti” plot where the averaged vibration mobilities for each measured part are plotted separately along a combined corpus (top+ribs+back) curve ( Figure 5). Usually the averaged radiativity (= pressure/force) curve computed by averaging the microphone pressure measurements over a sphere is also included. By looking at all the curves simultaneously it is possible to state that the small violin parts like the bridge, tailpiece and neck-fingerboard do not radiate sound. It is also straightforward to see which cavity or corpus modes radiate well from such a plot. An example spaghetti plot is shown for the Plowden (note that no bridge, tailpiece and neck-fingerboard motions were measured so plot is somewhat simpler than usual).
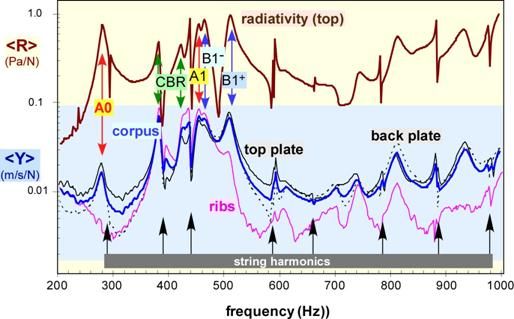
Figure 5 – “Spaghetti” diagram (partial) showing top, back and ribs and area-weighted-average corpus (top+ribs+back) out-of-plane rms mobilities for Plowden Guarneri del Gesu (1735) along with rms top hemisphere radiativity. Certain modes readily identifiable for every violin measured to date (signature modes), i.e., A0 (Helmholtz cavity mode), A1 (1st longitudinal cavity mode), plus the corpus modes labeled CBR, B1 - and B1 + are shown. The B1 modes are the strongest radiating corpus modes in the open string pitch region (196-660 Hz). A1 (from cavity-mode-induced-surface-motion) radiation is exceptionally strong for this violin (actually the strongest of 17 violins measured to date). Top plates generally are more active than back, while ribs are generally less active than both except in the 400-600 Hz region.
RESULTS
a. Total Damping
The OP mobility and radiativity curves shown in Figure 5 are not exceptional compared to those obtained for 12 other modern violins, signaling nothing unusual in the ability of old Italian violins to convert string vibrational energy into corpus vibration or radiated sound. However the widths of the peaks – a direct measure of the total damping - are generally somewhat greater than those measured previously for 12 modern violins up to about 2 kHz. The variability of the data is such that the total damping in any particular frequency region has overlapping error bars, so no statistical significance can be attached to any individual region, so this is just a general observation.
b. OP/IP Ratio and Directivity
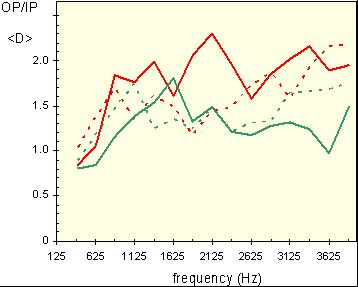
When the ratio of out-of-plane (OP) to in-plane (IP) mobility was extracted for the first time over the frequency range of 0-5 kHz for the two violins that had top and back plates measured there was an interesting result . The maple back plates for the Titian Stradivari and the Plowden Guarneri del Gesu all had similar OP/IP ratios, nominally about 3-4, decreasing slowly with frequency and very similar between the two old Italians. Contrast this with the results for the top plates as shown in Figure 6 ; the Titian averaged OP/IP mobility ratio was overall significantly higher than the Plowden. Even more interesting is the comparison of these OP/IP ratios with the computed directivity (= averaged top/back hemisphere pressure ratio) trends also shown in Figure 6 . The Titian has the larger directivity, and the largest overall of 17 violins of varying quality tested to date. It is worthwhile noting that the Willemotte Stradivari had the lowest directivity of any violin measured to date, so high directivity is not a Strad family property. It is however a valuable property for a soloist trying to compete with an orchestra.
WHAT CAN WE GET FROM THESE MEASUREMENTS?
These first 3-D measurements in toto combined with the acoustic measurements and the CT scans of these violins allow us to investigate important scientific questions about these old Italian vs. modern violins. Even though our talk does not cover most of the matters listed below, a short list of things we have measured or extracted from analysis for these old Italians includes:
One of the really difficult aspects of trying to understand these old Italian violins is our ability to characterize the materials used in the construction. While CT scans give you the absolutely necessary density information, equally necessary to understand vibrations are the stiffness properties of the wood. Is 3 century old wood the same as modern violin wood in density and stiffness? By combining our measurements of violin vibrational properties with the shape and density data from the CT scans in a computer simulation solid model we can actually extract information about the wood’s stiffness properties. In this way the complementary vibration and material information will make it possible in the not-too-distant future to create a solid model of an individual violin that is capable of simulating the measured properties listed above.
CONCLUSION
Shells in general are a very difficult scientific problem even for relatively simple geometries. And the difficulty is compounded by the fact that when IP waves reach discontinuities like the ribs or bassbar they can be converted to OP vibrations that do radiate well. These first 3-D measurements have given us insights into violin motion at a level never previously attained. They have improved our understanding of how strong in-plane vibrations are for the violin vs. out-of-plane vibrations. The OP/IP ratio has given us an uncomplicated parameter to help gauge how some violins become more capable of directing sound out into the auditorium than others.