


[ Lay Language Paper Index | Press Room ]
Popular version of paper 3pID2
Presented Wednesday afternoon, June 06, 2007
153rd ASA Meeting, Salt Lake City, UT
Sound morphing implies a gradual transformation from one sound into another sound, or the transfer of features of one sound onto another sound. Morphing can be used to generate hybrid timbres, sounds having characteristics of two different musical instruments (for example, the attack of an acoustic bass with the sustain and release of a bassoon, or the onset of a cello and the decay and beating of a piano) and sounds that evolve from one to another (one speaker evolving into another, or a cat evolving into a trombone). Morphing has been used to synthesize the voices of aliens and animals and a variety of sound effects in films and popular music.

Figure 1. Aire y agua I (M.C. Escher) depicts a gradual transformation from a sequence of birds to a sequence of fish.
Many soundfile editors (such as Audacity, shown in Figure 2 below) provide a facility for gradually fading out one sound while gradually fading in another sound. Could this crossfading mechanism be used for morphing one sound into another?
Figure 2.
Screenshot showing a crossfade of two sounds in Audacity,
available at
audacity.sourceforge.net.
Listen to this example of a crossfade between a flute and a trumpet, and notice what happens in the region of the crossfade.
Both sources are clearly audible during the crossfade. Mixing is not the same as morphing. In a mix, all the source sounds are (ideally) individually perceivable in the final sound. This is why an ensemble recording can be made by mixing the signals from several microphones.
In a sound morph, only a single sound should be audible throughout the transformation. In this example, the flute and trumpet differed in pitch, so there was little chance that they would fuse into a single sound in the mix. Listen to this example of a crossfade between a flute and a trumpet having the same pitch.
This sounds slightly better, but both sources are still audible during the crossfade. Many sounds can be decomposed into their component sine waves. The frequency and amplitude of the sine waves (called harmonics, in the case of pitched sounds) vary over the duration of the sound. The original sound can be reconstructed by adding together all of the component sine waves.
Even sounds having the same pitch are individually perceivable in a mix, unless the individual component sine waves (harmonics) are tuned to exactly the same frequencies in the two sources. Listen to this example, in which the frequencies of the harmonics of the flute and trumpet have been synthetically aligned.
Now, only a single instrument tone is audible throughout. Perfectly-tuned harmonics such as these can be generated synthetically (using a computer or a music synthesizer, for example), but they do not occur naturally.
In order to artificially align the harmonics of one recorded sound to those of another, it is first necessary to determine the frequencies of those harmonics. Fortunately, a variety of techniques are available for determining the time-varying frequencies and amplitudes of the sine wave components of a sound, and modern methods work well for many sounds. In particular, we use a method called time-frequency reassignment to obtain sharper estimates of the time and frequency behavior of those components than is available using classical analysis techniques.
A sound analyzed in this way is plotted in Figure 3, below. Time increases from left to right, and frequency increases from bottom to top. Dark areas show regions in which energy is concentrated, and the harmonic components of the sound are clearly visible as dark, horizontal stripes. In a pitched sound, as in this example, the harmonic components are spaced approximately evenly in frequency. The lighter grey smudges between the dark stripes show regions of noisiness and non-harmonic energy in the sound.
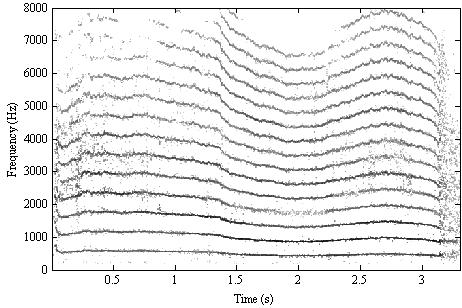
Figure 3. Time-frequency reassigned analysis of a cat meowing. Time (measured in seconds) increases from left to right, and frequency (measured in Hertz) increases from bottom to top. The harmonic components representing most of the energy in this sound are visible as dark horizontal stripes, spaced approximately evenly in frequency. The lighter grey smudges between the dark stripes show regions of noisiness and non-harmonic energy in the sound.
From such data, it is possible to construct a model of a sound as a collection of sine waves. A sound represented in this way is plotted in Figure 4, below. The individual components in the model are depicted as wiggly lines. As in Figure 3, above, time increases from left to right, and frequency increases from bottom to top. Louder components are plotted in darker grey, quieter ones in lighter grey.
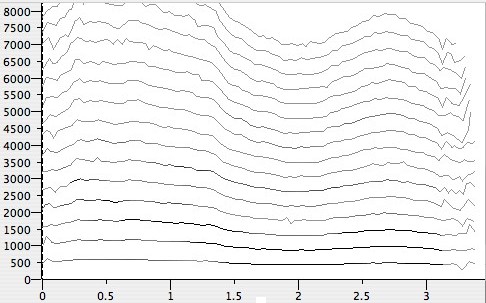
Figure 4.
Additive sound model data for a cat meowing, plotted using Spear
by Michael Klingbeil,
(available at
www.klingbeil.com/spear).
Time (measured in seconds) increases from left to right, and
frequency (measured in Hertz) increases from
bottom to top.
The individual components in the representation are depicted as
wiggly lines. Louder components are plotted in darker grey, quieter ones in
lighter grey.
It is a simple matter to reconstruct a sound from such a representation by synthesizing the individual sine waves and adding together the results (for this reason, these are often called additive sound models). Listen to a trumpet sound being constructed one sine wave at a time.
Listen to the cat meow, depicted in the figures above, reconstructed from additive model data.
Additive models afford intimate control over the evolution of a synthesized sound. For example, the sound can be stretched or compressed in time by changing the rate at which the sine wave parameters change. Listen to the effect of time-stretching on the cat meow (*).
The sound can be modified in various ways by modifying the parameters of the sine wave model. The pitch can be altered by systematically modifying the frequencies of the sine waves. The individual harmonics of a pair of sounds can be perfectly aligned, as in the trumpet-and-flute mixing example above. The additive model data can also be morphed directly.
Sound morphing can be performed by blending the parameters (amplitudes and frequencies) of the sine wave components in a pair of additive models. The sine wave frequencies do not need to be perfectly aligned in order to perform the morph. Rather, the raw additive model components can be morphed to produce a new morphed model from which the morphed sound is synthesized. A loud sine wave in one sound morphed with a quiet sine wave in another yields a sine wave of medium amplitude. A high frequency sine wave in one sound morphed with a low frequency sine wave in another yields a sine wave of intermediate frequency. This parameter blending operation is depicted in Figure 5, below, for a single morphed sine wave.
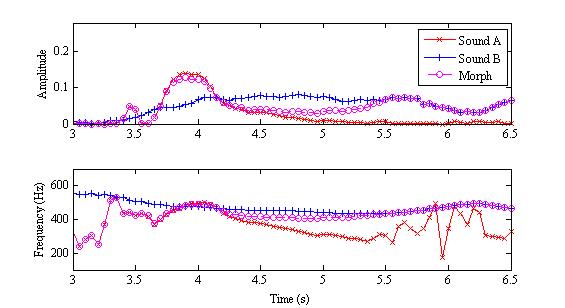
Figure 5. Plots showing morphing of amplitude (top plot) and frequency (middle plot) parameters for one component in a morph. The red 'x' shows the parameters for the one source sound, the blue '+' shows the parameters for the other source. The morphed parameters are shown in purple circles.
In this figure, the red 'x' shows the parameters for the sound at the start of the morph. The blue '+' shows the parameters for the sound at the end of the morph. The morphed parameters are shown in purple circles. The morph makes a gradual transition from the parameters of the first sound to those of the second.
Listen to this example of a viola tone morphed with a flute tone. The pitches of the two tones are slightly different, so it is easy to hear the transformation from the lower viola timbre to the higher flute timbre as the morph progresses.
Listen to this example of a piano tone morphed with a temple bell. The temple bell is not pitched, so it is not possible to align the harmonics (as in the trumpet-flute example) without dramatically altering the sound of the bell. Nonetheless, by carefully pairing the components in the two additive models, it is possible to achieve a pleasing morph between the two sounds.
Trevor Cox, a professor of acoustic engineering at Salford University, conducted a year-long study to identify the world's worst sound, and to determine what makes certain noises so objectionable. You can read about the study and its results on The Guardian website, or visit www.sound101.org.
We have collected a few of the sounds used in Professor Cox's study, and attempted to "rehabilitate" them by morphing them with other, less-horrible sounds, or, at least, more entertaining ones. Some examples are included here.
Here is an example of a crying baby morphed into a piano.
Here are examples of several morphs performed using the sound of a meowing cat (*).
Not surprisingly, we found that morphing two awful sounds (the crying baby and the meowing cat, in this case) does not improve either of them.
In this last example, a metalic scraping sound is transformed into a flexitone (a percussion instrument sometimes used to make eerie sound effects).
This work has been conducted with Dr. Lippold Haken from the Department of Electrical and Computer Engineering at the University of Illinois in Urbana-Champaign.
All sound morphs presented here were created using the Loris software for sound analysis, synthesis, and manipulation, available at the Loris website.
For more information, contact the author, or visit Kelly's website.
(*) No animals were harmed in the preparation of this paper.