Acoustical Society of America
159th Meeting Lay Language Papers

The Banjo: the Science Behind the Sound

Joe Dickey - Joe@JoeDickey.com
3960 Birdsville Rd.
Davidsonville, MD 21039

Popular version of papers 3aMU4 and 3aMU5
Presented Wednesday morning, April 21, 2010
159th ASA Meeting, Baltimore, MD


Heres how a physicist looks at a banjo.



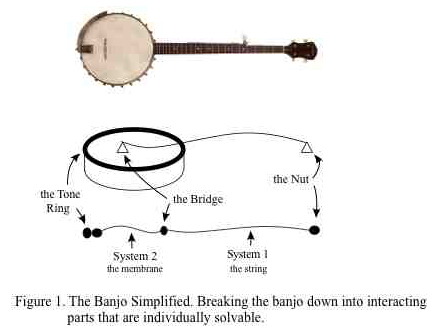
The simplified banjo is basically composed of two interacting vibrating systems: a plucked string and a circular membrane. The five-string banjo is a little more complicated, as it has six interacting systems -- five strings and one membrane. By interacting we mean that waves in the string generate waves in the membrane, and visa versa, so that the whole instrument vibrates. From basic physics, we can write and solve the equations which describe the way waves travel in these systems, how they radiate sound and how they interact. Why do we do this? Partly to build better banjos; but, more generally, to build a better anything. This story describes the way a lot of physics is done.

First the strings. Given the tension in the string (provided by the tuning peg) and its mass (gauge) we know how an initial displacement (a pluck) travels and reflects off the ends. We call this a structural vibration, or a wave, and this wave will travel back and forth in the string reflecting alternately from one end and the other. And just as it takes some force to contain the end of a jumping rope, it takes force to keep the string connected (through the bridge) to the membrane. We can calculate all of this.



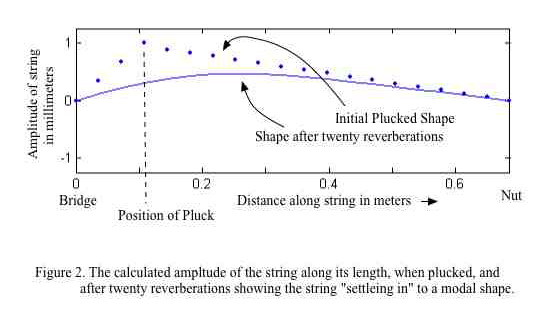
Figure 2 shows a pluck, initially a triangular shaped displacement shown as a dotted line. The vertical scale in the figure is greatly exaggerated to make it easier to see what is going on. Normally, the displacement of the string is only about one-thousandth of its length. The figure also shows what the string shape would be after about 20 reverberations. Note that the response of the string has diminished in time because there has been energy shared with the other systems and because all the systems have losses. Note, also, that the triangular shape of the pluck has smoothed to the point of looking like our jumping rope; specifically, it resembles the sinusoidal shape we generally expect from a vibrating string. More importantly, the string settles into vibrating at a specific frequency that we hear as a particular note. We call this a mode, and the settling-in of the pluck to this mode is more apparent in the slow motion movie version of the evolution of the pluck in time.

Click HERE to watch a video and see this.

Finally, the settling- in process takes only a small fraction of a second and during that time, the vibration is not modal and, therefore, not a well defined note. This is the twang.

Next the membrane. Like the string, the membrane is also under tension and has mass but in this case waves travel as circles expanding outwardly from their origin rather than along a line. This would be orderly enough except that their origin (the bridge) is not in the center of the circle. As a result, different parts of the expanding wave meet the boundary (the tone ring) at different times. Its much easier to visualize this added complexity by looking at the propagation of a very short wave. Such a wave would be impossible to generate experimentally, but in the world of mathematics, we can do pretty much anything.



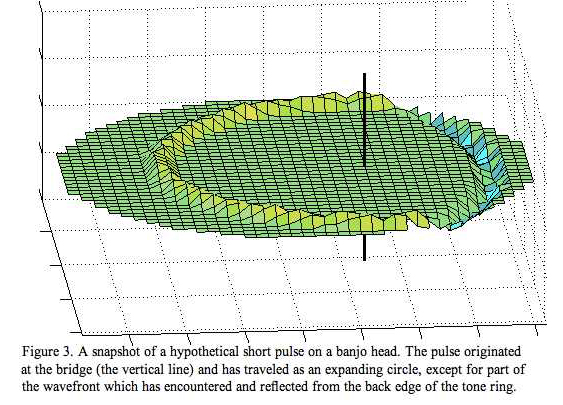
Given this, Figure 3 shows a snapshot of such a (calculated) wave which has left the source and traveled to a point where part of the wavefront has reflected from the tone ring. Again, the complexity is better appreciated in the time evolution movie: click HERE.

Note that the vertical scale is exaggerated and that the pulse goes from positive amplitude (i.e. upward) to negative (downward), and visa versa, at every reflection. Also, keep in mind that the wave looses energy (and amplitude) as it travels and when it encounters either the tone ring or the bridge.

Replacing the short pulse with a more realistic excitation imparted to the head by the string, we get head displacements which look quite different and are, in fact, similar to measured results. The time evolution of a representative situation is shown HERE.

Again, the time span for the movie is a fraction of a second.

Finally, the sound. A significant, and certainly the most pertinent energy loss to the membrane waves is the energy radiated as sound. As a section of the membrane moves up, it pushes and condenses the air above it causing a slight increase in ambient pressure, and as it subsequently moves down, it forms a rarefaction, a slight decrease from ambient pressure. This alternating pressure/rarefaction is, by definition, a sound wave.

So there you have it; summarized in a sentence. A string held at both ends is plucked; it interacts with and causes waves in a membrane, which radiates sound. It may seem like a lot of trouble for something which can be summarized in one sentence; but heres the deal. Once the model is on the computer, it takes only a few seconds to calculate allowing you to easily change things like head tension, string gauge, bridge mass, etc. to see what happens to the sound.

And now the bad news. Real world systems are generally too complicated to be modeled accurately. There are a number of simplifying assumptions in this and essentially all physical models. Also, in the case of musical instruments, physical models compete with the most sophisticated acoustic analyzer of all: the ear. Models and experiments are a long way from discerning the subtleties of good tone. The evolution of good tone in musical instruments has been largely trial and error and, as such, has been a slow process. Physical modeling offers a useful tool to estimate the sensitivity of tonal parameters to proposed design changes and possibly shorten the design cycle. There is sound at the end of the tunnel.