Listen to Bone Quality:
How Ultrasound Helps to Reveal Microstructure and Elastic Function in Bone
Kay Raum -
kay.raum@charite.de
Julius
Wolff Institute & Berlin-Brandenburg School for Regenerative Therapies
Charit
- Universittsmedizin Berlin
Augustenburger
Platz 1
13353 Berlin, Germany
Quentin Grimal -
quentin.grimal@upmc.fr
Laboratoire dImagerie Paramtrique
CNRS, Universit Pierre et Marie Curie-Paris 6
F75006
Paris, France
Alf
Gerisch - gerisch@mathematik.tu-darmstadt.de
Fachbereich
Mathematik
Technische
Universitt Darmstadt
Dolivostr. 15
64293
Darmstadt, Germany
Pascal Laugier -
pascal.laugier@upmc.fr
Laboratoire dImagerie Paramtrique
CNRS, Universit Pierre et Marie Curie-Paris 6
F75006 Paris, France
Popular version of paper 5pBB9
Presented Friday afternoon,
April 23, 2010
159th ASA Meeting, Baltimore,
MD
Introduction
Sophisticated technical materials that are used in
everyday life are often inspired by nature. Lightweight honeycomb constructions
and carbon fiber reinforced sandwich composites, for example, are used to
construct airplanes, cars or modern sports equipment and aim to optimize
various properties, e.g. weight, toughness and strength that cannot be achieved
by a single material. Examples of adopting structural concepts from nature for
the design of technical materials and the construction of devices date back
centuries, to the first concept of a flying machine by Leonardo da Vinci in 1488. However, our current knowledge about
natural concepts to achieve a desired function is still limited and the
investigation of functional consequences of specific design variations is the
focus of the rather young and growing research discipline, called Biomimetics.
Hard biological tissues, e.g. mineralized tendons,
bone and teeth are natural examples of achieving unique combinations and also
great variability of stiffness and strength. All of these tissues have a common
building block a collagen fibril that is reinforced by small mineral
crystals. One of the striking features of these tissues is the ability to adapt
to variable loading conditions by multiple but well organized structural
arrangements of this building block at several levels of hierarchical
organization (Fig. 1).
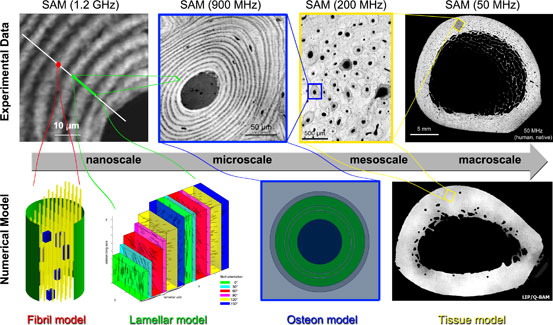
Figure 1. Hierarchical structure of compact bone: a) compact
bone in long diaphysis; b) osteons
formed by lamellae; c) bone lamellae, made of a sandwich compound of
mineralized collagen fibril films with variable orientations; d) film of
mineralized collagen fibrils with a single orientation e) basic building block:
the mineralized collagen fibril; f) extra-fibrillar
matrix. From Reisinger et al. [1].
For survival, the skeleton of animals and humans has
to provide stability, support and protection of the internal organs against
mechanical impacts in combination with the ability of fast and energy efficient
locomotion that is needed to collect food, hunt or escape from other hunting
animals. Moreover, this functionality has to be preserved throughout lifetime,
which requires adaptation to variable conditions during maturation and ageing,
but also repair mechanisms that allow both, an incremental repair of microdamage and restoration of macroscopic defects, i.e.
fractures.
In order to achieve these goals, bone uses various
design concepts, e.g. reinforcing a soft and flexible collagen matrix by stiff,
but brittle mineral particles, sandwich compounding of anisotropic
(directional) films, weight reduction by directional pores and spongy networks.
Adaptation and repair is realized by an army of cells specialized either in
sensing, mining or construction of bone tissue. Altogether this leads to a
highly dynamic, lightweight stiff and tough compound material that is usually
able to maintain its function throughout lifetime.
This principle of bone adaptation is widely accepted
as Wolffs law of bone adaptation based on the
classic work of Julius Wolff entitled Das Gesetz der Transformation der Knochen (The Law of Transformation of Bone),
published in 1892 [2]. Since then mechanical properties of bone have been
intensively investigated by macroscopic to nanoscopic
mechanical testing, imaging and numerical approaches.
Although many details of the genetics, biology,
pathology and mechanics of bone have been uncovered, we still lack of a
detailed understanding of bone structure at the nano-
and microscales. Existing theoretical bone models
only allow us a limited description of macroscopic function (e.g. stability and
resistance to failure) based on structural and compositional features at
smaller hierarchical levels of organization. However, such models are crucial,
e.g. to i) understand the mechanical and biological
mechanisms of bone adaptation, ii) predict the outcome of anabolic (bone
building) or antiresorptive treatment strategies,
iii) define design concepts for technical materials with equally good combinations
of properties like bone and iv) provide a better understanding of the origin of
the mechanical resistance properties of bones. The latter is of particular
importance, as it would help researchers to design a new class of non-invasive,
non-ionizing, ultrasound based diagnostic systems that would allow for a safe
and reliable prediction and monitoring of fracture risk and fracture healing.
Towards this goal, both experimental data of
heterogeneous elastic and structural parameters from all length scales (from
the centimeter to the nanometer scale) and theoretical models that can simulate
the deformation behavior based on these data are required.
Quantitative Ultrasound
If sound waves propagate through a material, their
elastic interactions cause small reversible deformations (compression,
expansion, or shearing). The velocities of these deformations are determined by
the elastic properties and the mass density of the material. This principle has
been used for decades for the non-invasive and nondestructive evaluation of
technical materials and biological tissues [3-6]. Focused ultrasound
transducers that emit short pulses and measure the reflection amplitude can be
used like a virtual fingertip to probe the elastic response of the surface of
a material. By scanning the transducer over the surface, elastic maps can be
obtained. The size of this virtual fingertip depends upon the numerical
aperture of the sound field and the acoustic frequency, and can be varied over
several orders of magnitude (from 10 mm at 100 kHz down to 0.5 m at 2 GHz)
[7-14].
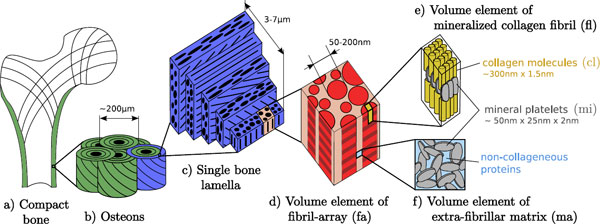
Figure 2. Acoustic images (top) and numerical models (bottom)
of human bone cross-sections. The gray-scale in the acoustic images corresponds
to the local elastic response of the tissue to the incoming wave (bright =
stiff; dark = soft). From left to right:
Ultrasound in the GHz range reveals the apparent sandwich compound
structure of fibril bundles. The large dark spot is a Haversian
canal hosting blood vessels and the small spots are osteocyte
lacunae, hosting bone cells. These data (in combination with other input data)
are used to construct the fibril, lamellar, and osteon
models. At 200 MHz parallel and elliptical tissue structures (osteons) as well as a porous microstructure can be
observed. These data are the basis for the tissue model.
The Bottom-up Approach
A bottom-up approach requires experimentally
assessed structural, compositional and elastic data at each hierarchical level
of organization from the nanoscale to the macroscale (Fig. 2). These data can be obtained by
ultrasound with the frequency tuned to the structural dimension at each
hierarchy level and site-matched complementary data (e.g. mineralization from
synchrotron radiation micro computed tomography (SR-CT) [7, 8, 10, 11].
Simplified volume elements that resemble the major structural design features,
but also incorporate degrees of freedom for dynamic adaptation (e.g. a
time-dependent change of mineralization) can then be constructed (Fig. 2). The
effective elastic properties of such volume elements can be computed by
numerical homogenization approaches [15, 16]. For example, the data can be
translated into a so-called Finite Element (FE) mesh. By numerical deformation
analyses, i.e. a virtual compression and calculation of the resulting
deformation, the elastic parameters that describe a similarly behaving
homogeneous material, i.e. a material without any structure or variation of
material properties, can be derived.
Homogenization from the nano-
to the macroscale is performed in a series of steps:
the effective material properties obtained at one hierarchical level are used
to build the volume element at the next scale. The advantage of this approach
is a dramatic reduction of complexity without the loss of structure-functional
relationships. Furthermore, experimental data at a given next length scale
serve both for the validation of the homogenization model and as input for the
next homogenization step.
Results
We have derived the elastic stiffness parameters, i.e.
the elastic stiffness tensor and the degree of mineralization in human cortical
bone at several length scales by site-matched Scanning Acoustic Microscopy
(SAM) and SR-CT. From these data, hierarchical models have been developed that
connect the nanoscale with the macroscale
(Fig. 2) and describe the elastic behavior of the tissue at all length scales.
Our results indicate that some of the previously proposed fibril arrangements
at the nanoscale [17] do not result in the
experimentally observed elastic properties at the next length scale (microscale). However, our data support the model of a
twisted plywood structure [18, 19]. This model
uses only a simple construction rule, but allows in principle the design of
several previously reported fibril arrangements by a variation of the thickness
of individual fibril layers. At the next length scale (mesoscale),
the effects of material properties and the porous network have been evaluated
numerically. Moreover, local variations of the mesoscale
structural and elastic properties within the femoral shaft appear to be related
to an inhomogeneous strain distribution resulting from external (macroscopic)
stresses by weight and muscle forces.
Conclusion
Ultrasound provides a unique and to date almost
unexplored way to listen to bone quality. In contrast to other mechanical or
imaging techniques, this ultrasound-based elastic imaging approach combines the
possibility to assess structural and material properties of the tissue across
multiple length scales. In order to handle this complex information,
established engineering tools, e.g. finite element analyses and homogenization
techniques have been employed. By utilizing such a combination, the principal
mechanisms leading to the exceptional combination of toughness and strength, as
well as the change of these properties throughout the course of bone ageing or
pathologies, can be investigated.
Acknowledgments
This work has been conducted within the European
Associated Laboratory Ultrasound Based Assessment of Bone (ULAB) and was
supported by the Deutsche Forschungsgemeinschaft
within the priority program SPP1420 Biomimetic
Materials Research: Functionality by Hierarchical Structuring of Materials
(grant Ra1380/7).
References
[1] Reisinger,A.G., Pahr,D.H., Zysset,P.K., Sensitivity analysis and parametric study of
elastic properties of an unidirectional mineralized bone fibril-array using
mean field methods, Biomech. Model. Mechanobiol. 2010.
[2]
Wolff,J.,
Das Gesetz der Transformation der Knochen. Berlin, Verlag von August
Hirschwald. 1892.
[3] Ashman,R.B., Cowin,S.C., Rho,J.Y., Van Buskirk,W.C., Rice,J.C., A continous wave
technique for the measurement of the elastic properties of cortical bone, J. Biomech. 17 (5), 1984, 349-361.
[4] Lees,S., Heeley,J.D., Cleary,P.F., A study of some properties of a sample of
bovine cortical bone using ultrasound, Calcif. Tissue
Int. 29 (2), 1979, 107-117.
[5] Rho,J.Y., An ultrasonic method for measuring the elastic
properties of human tibial cortical and cancellous bone, Ultrasonics 34 (8), 1996, 777-783.
[6] Van Buskirk,W.C., Cowin,S.C., Ward,R.N., Ultrasonic measurement of orthotropic elastic
constants of bovine femoral bone, J. Biomech. Eng.
103 (2), 1981, 67-72.
[7] Raum,K., Microelastic imaging of
bone, IEEE Trans. Ultrason. , Ferroelect.
, Freq. Contr. 55 (7), 2008, 1417-1431.
[8] Raum,K., Hofmann,T., Leguerney,I., Saied,A., Peyrin,F., Vico,L., Laugier,P., Variations of microstructure, mineral density
and tissue elasticity in B6/C3H mice, Bone 41 (6), 2007, 1017-1024.
[9] Raum,K., Kempf,K., Hein,H.J., Schubert,J., Maurer,P., Preservation of microelastic
properties of dentin and tooth enamel in vitro--a scanning acoustic microscopy
study, Dent. Mater. 23 (10), 2007, 1221-1228.
[10] Raum,K., Leguerney,I., Chandelier,F., Talmant,M., Saied,A., Peyrin,F., Laugier,P., Site-matched assessment of structural and
tissue properties of cortical bone using scanning acoustic microscopy and
synchrotron radiation CT, Phys. Med. Biol. 51 (3), 2006, 733-746.
[11] Hofmann,T., Heyroth,F., Meinhard,H., Franzel,W., Raum,K., Assessment of composition and anisotropic elastic
properties of secondary osteon lamellae, J Biomech. 39 (12), 2006, 2284-2294.
[12] Hube,R., Mayr,H., Hein,W., Raum,K., Prediction of
biomechanical stability after callus distraction by high resolution scanning
acoustic microscopy, Ultrasound Med. Biol. 32 (12), 2006, 1913-1921.
[13] Raum,K., Leguerney,I., Chandelier,F., Bossy,E., Talmant,M., Saied,A., Peyrin,F., Laugier,P., Bone
microstructure and elastic tissue properties are reflected in QUS axial
transmission measurements, Ultrasound Med. Biol. 31 (9), 2005, 1225-1235.
[14] Raum,K., Jenderka,K.V., Klemenz,A., Brandt,J., Multilayer
analysis: Quantitative scanning acoustic microscopy for tissue characterization
at a microscopic scale, IEEE Trans. Ultrason. , Ferroelect. , Freq. Contr. 50 (5), 2003, 507-516.
[15] Parnell,W.J., Grimal,Q., The
influence of mesoscale porosity on cortical bone
anisotropy. Investigations via asymptotic homogenization, J R. Soc. Interface 6
(30), 2009, 97-109.
[16] Grimal,Q., Raum,K., Gerisch,A., Laugier,P.,
Derivation of the mesoscopic elasticity tensor of
cortical bone from quantitative impedance images at the micron scale, Comput. Methods Biomech. Biomed Engin. 11 (2), 2008, 147-157.
[17] Wagermaier,W., Gupta,H.S., Gourrier,A., Burghammer,M., Roschger,P., Fratzl,P., Spiral
twisting of fiber orientation inside bone lamellae, Biointerphases
1 (1), 2006, 1-5.
[18] Giraud-Guille,M.M., Besseau,L., Martin,R., Liquid crystalline assemblies of collagen in
bone and in vitro systems, J. Biomech. 36 (10), 2003,
1571-1579.
[19] Giraud-Guille,M.M., Twisted plywood architecture of collagen
fibrils in human compact bone osteons, Calcif. Tissue Int. 42 (3), 1988, 167-180.