Glass Breakage by Blasts - A Prediction Model and Real-world Validation

 

Louis C. Sutherland - lou-sutherland@juno.com

LCS Acoustics

Rancho Palos Verdes, CA

 

Popular version of paper 3pNS2

Presented Wednesday afternoon, April 21, 2010

159th ASA Meeting, Baltimore, MD

 

 

It is not surprising that windows are usually the structural element in a building most subject to damage by the overpressure pulse from an explosion. After all, what other building element can so easily be broken by a baseball hit by an unlucky young batter in a neighborhood baseball game played too close to your home. A powerful statistical model for damage to windows from similar impulsive pressure loads was developed in 1976 by R.L Hershey and T.H. Higgins for the FAA in a study concerning window damage from sonic booms. This model was used to predict the statistical probability of damage to windows in an apartment complex exposed to blast overpressure from a accidental explosion of a small, solid rocket motor undergoing a vibration test in a nearby environmental test facility. The apartment complex consisted of 9 buildings with 738 windows located at distances of 430 to 980 ft from the blast source as portrayed below in Fig. 1. The windows faced different directions relative to the incident blast wave with most of the 53 broken windows facing the blast source. Fortunately, no one was injured by this blast.

 

This paper reviews the blast loading on the windows which faced different directions relative to the incident blast wave, the resulting blast-generated structural stress in the windows and the statistical prediction of damage to these windows from this blast.

 

Based on the 20 lb weight of the rocket motor, a knowledgeable explosions expert estimated the blast was equivalent to a charge of about 30 lb of TNT.

 

The expected time history of the pressure pulse from such a TNT charge at a distance to a typical window, located at 710 ft., is shown in Fig. 2 along with the predicted surface velocity, due to the blast, at the center of this window. The blast pulse time history is characterized by two key parameters, the peak incident pressure, P_o (0.1 psi) and the duration, T₊ (0.02 sec.) of the positive pressure phase of the blast pulse.

 

The structural velocity at the center of the glass pane exhibits the characteristic sinusoidal-type vibration expected for a structure vibrating in all its resonant modes. The fundamental frequency for vibration of the window pane was calculated to be 24 Hertz (cycles per second) for the 28 x 27 in. window.

 

From well-verified blast prediction models, the peak effective blast pressure at the face of this window, including a 2 to 1 blast pressure reflection factor at the window surface, was estimated to be 0.2 lbs per square inch. This corresponds to a peak sound pressure level of about 156 dB.

 

 

 

 

 

 

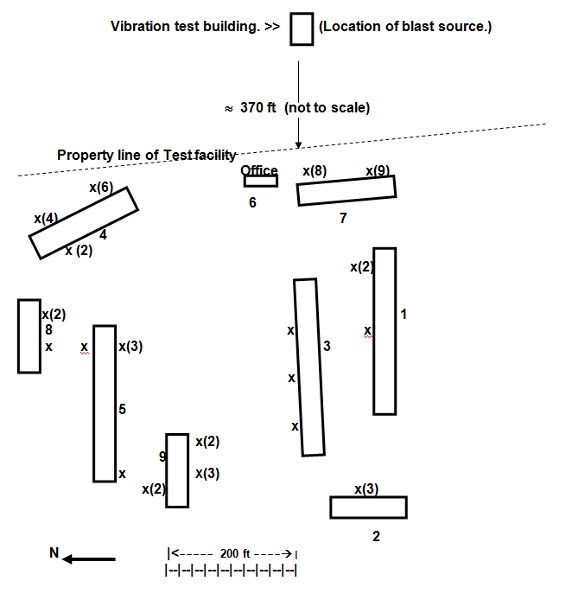
Figure 1. Geometry of Vibration test stand and the nine buildings of the nearby apartment complex. The xs designate the approximate location of the broken windows and the number in ( ) indicates the number broken at his location. (No number indicates just 1 window broken at the x location.)

 

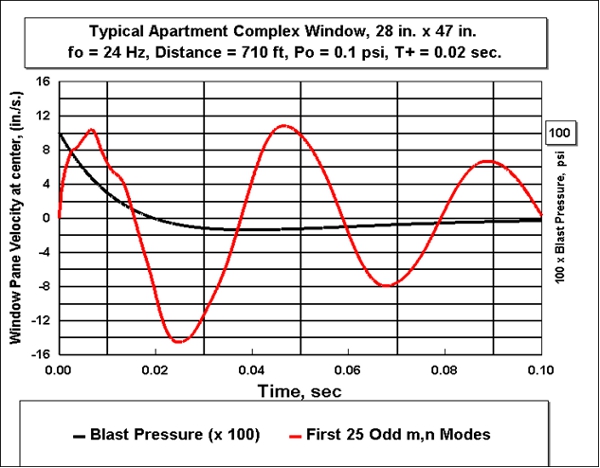
Figure 2. Time history of blast pressure and structural velocity at surface of a typical window in the apartment complex due to the accidental explosion from 30 lbs of TNT located 710 ft. from the window which was facing the incident blast wave.

 

The structural velocity at the surface of the window panes is used to predict the dynamic stress in the windows due to the incident blast wave. This utilizes a powerful relationship between the peak stress, S_pk in a sinusoidally vibrating structure and its peak structural velocity, V_pk that was first developed by the late Prof. F.V. Hunt in 1960. Essentially the relationship states that:

 

S_pk = K_S [ V_pk,/ C_L] psi (1)

 

where

K_S = a vibration/stress proportionality factor dependent on the geometry of the structure and Youngs Modulus of Elasticity, in psi of the material

C_L = the longitudinal speed of sound, in the material in in/s and

V_pk = the peak modal velocity, in in/s.

(Note, that (V_pk/C_L) could be considered as a structural response Mach No.)

 

The peak structural stress, S_pk varies directly with the peak effective blast pressure, P_eff acting on the window, the dynamic response characteristics of the window, e,g, its resonance frequencies and its surface weight all predictable quantities. The risk of damage to the window is defined the Factor of Safety (FOS) involved in the window blast exposure of the window to the blast. This FOS is simply the ratio of the threshold for damaging stress, S_d for the window material to the peak stress, S_pk imposed by the blast or,

 

FOS = S_d / S_pk (2)

All factors involved in each of part of this ratio can be estimated in terms of their nominal value and the standard deviation about this nominal mean value. The statistical distribution of the stress threshold for damage of window glass was especially well defined from extensive published data. The net result is that the Factor Safety (FOS) also has a statistical distribution and a standard deviation, s_FOS, which is the root mean of the standard deviation of all the terms making up the ratio in Eq. (2).

 

It turns out that the logarithm of the FOS has, what is called a Normal Distribution that has the haystack shape shown below. Damage to a window is presumed to occur when ever the FOS is less than 1 or the Log of the FOS is less than 0. Thus, the Probability of Damage (POD) for this illustration is equal to the area under this normal distribution of the Log of the FOS for which this Log is less than 0 which is 7.3 %, for this illustration.

 

 

 

 

 

 

 

 

 

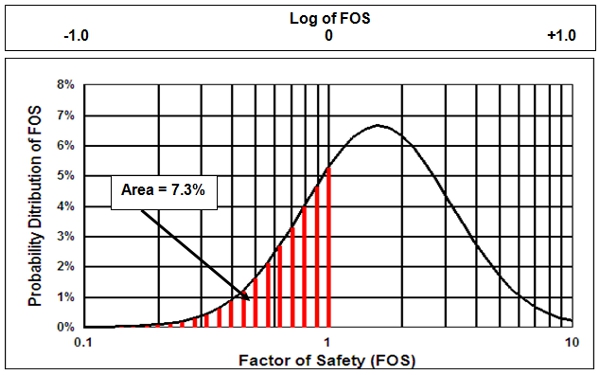
Figure 3. Illustration of normal distribution of Log of Factor of Safety (FOS). Total Probability of Damage (POD) of 7.3 % is represented by the crosshatched area under that part of the Lg[FOS] distribution for which the FOS 1 or Lg[FOS] is 0.

This prediction of the POD for the windows in the Apartment Complex utilized well-known math models for the Normal Distribution and statistical distribution data for all the terms involved in Eq. (2), including model data, not discussed here, on the change in effective sound levels on the front, side and back of buildings simulating the blast wave reflection effects for the windows in the Apartment Complex. The average observed and predicted POD for the windows on the front, side and back of the buildings relative to the blast incidence direction are shown in Fig. 4 to be in good agreement.

 

 

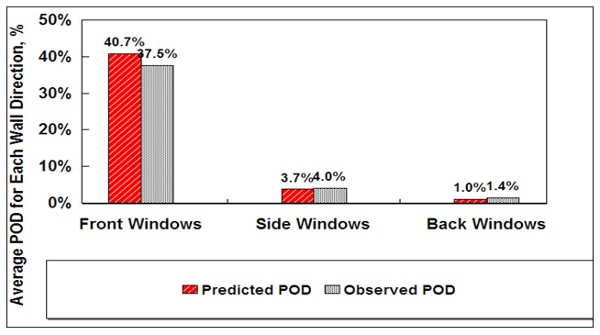
Figure 4. Average N-weighted, predicted versus observed POD for the window orientation re: the blast direction for N = 80 front, N = 520 side and N = 138 back windows.

 

The Fig. compares the average predicted and observed window failure rates for each of the three window directions The agreement provides support for the basic validity of the structural damage prediction model employed for this study.