Christie A. O’Hara – christie.ohara@jhuapl.edu
Johns Hopkins University, Applied Physics Lab
11100 Johns Hopkins Rd.
Laurel, MD 20723
Jon M. Collis – jcollis@mines.edu
Colorado School of Mines
1500 Illinois St.
Golden, CO 80401
Popular version of paper 4aUWc
Presented Tuesday morning, November 1, 2011
162nd ASA Meeting, San Diego, Calif.
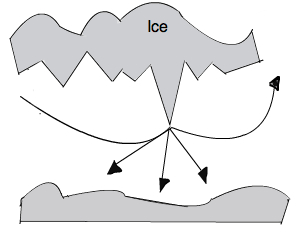
Developments in underwater acoustic modeling for the Arctic region have been limited due to the complicated nature of the polar extreme. In the Arctic, unlike warmer waters, areas can be covered with an ice cover or just have a layer of colder water at the surface. The low surface temperature causes sound to bend upward and reflect off the underside of the ice. This upward refracting sound speed profile causes any long-range sound transmissions to repeatedly interact with the ice cover. At lower frequencies (such as deep bass sounds) the distance the sound wave travels is much larger than the average depth of the ice keels and the jagged ice cover does not play a significant role. However, at higher frequencies (such as humans speaking) the jagged ice cover can cause a sound wave to break up into multiple sound waves. This scattering effect is depicted in Figure 1. The subsequent break up of the initial sounds wave into numerous waves thus poses a challenge for accurately modeling sound as it propagates to long distances. One peculiarity of Arctic sound transmission is that both high and low frequency signals weaken rapidly: the former by reflection losses from the ice cover; the latter due to the fact that very low frequency sounds are not trapped effectively in the ocean and then interact with the ocean bottom where bottom loss can be significant. The focus of this paper is on low frequency sound propagation, 20 Hz, where the effect of the ice is small and will assume a flat ocean surface boundary as an initial approximation to the Arctic surface environment.

Figure 1: Sound propagation paths in the Arctic. The propagation paths are subject to scattering loss at the rough underside of the ice.
Much of the research in the Arctic has been in the fields of climate observation, underwater acoustic communication and navigation, acoustic tomography (inversion of temperature profiles) and thermometry (temperature studies), and bioacoustics (the study of acoustics in biological settings). However, sound propagation data from the Arctic Ocean, especially in deep-water environments, are very scarce.
Recently, noticeably warmer ocean temperatures have led to an increased interest in the Arctic region due to the associated decreasing presence of Arctic sea ice. The diminishment of sea ice, which for decades has served as an impediment to maritime activity, could allow for increased exploration of oil, gas, and minerals, as well as the establishment of new shipping routes. In view of these changes, the U.S. Navy has increased its interest in the Arctic region based on its need to have the capability to detect long-range signals and noise. Specifically, this capability will enable naval assets to predict transmission loss, the acoustic pressure that is lost in transmitting a signal from one point to another, for detection and communication.
Computational models have been used extensively to advance our understanding of underwater acoustic propagation. A generic ocean acoustic propagation scenario involves interaction with both the sea surface and ocean bottom interface boundaries. A simplified model of the Arctic Ocean acoustic environment is referred to in this work as a ‘modified Pekeris waveguide,’ which is a physical structure (the Arctic ocean) for guiding sound waves. The bottom is considered to be an infinite fluid layer and the top is considered to be a fluid layer of finite thickness overlaying the water column, in which a sound source is present. For modeling purposes, a first approximation to the real ocean acoustic environment is to consider it range independent, that is to assume that environmental parameters such as sound speed, water depth, and bottom and top composition are invariant in the primary direction of propagation (horizontal) and are only functions of water depth. In addition, the media of propagation are assumed to be homogenous (constant sound speed and density) fluid layers. In this talk, a mathematical solution for this simplified environment is validated against experimental data to check for accuracy.
Figure 2 shows transmission loss versus range for a receiver depth of 90 m comparing the modified Pekris waveguide (solid curve) and experimental data (dashed curve). These measurements were made by deploying SUS charges (small, 1.8 pound explosives with known source levels, that the Navy designed for finding submarines) from an airplane into leads (stretches of open water) in the ice field [1]. The resultant data was processed over a small band of frequencies (1/3 octave) to average out signal variations. Transmission loss was calculated at ranges between 0 km to 500 km and features an ice layer that is 5 m thick and a water layer, that includes the concurrently measured sound speed profile, over an infinite bottom sediment layer. Calculations were averaged over a 1/3 octave to be consistent with measurements. The theoretical calculations shown in this figure are consistent to spherical spreading at ranges less than one water depth, and cylindrical spreading at greater ranges, as might be expected from a experience based model. Furthermore, our calculations are generally consistent with measurements. The small discrepancies evident at increasing ranges are due to attenuation due to sea ice [2].
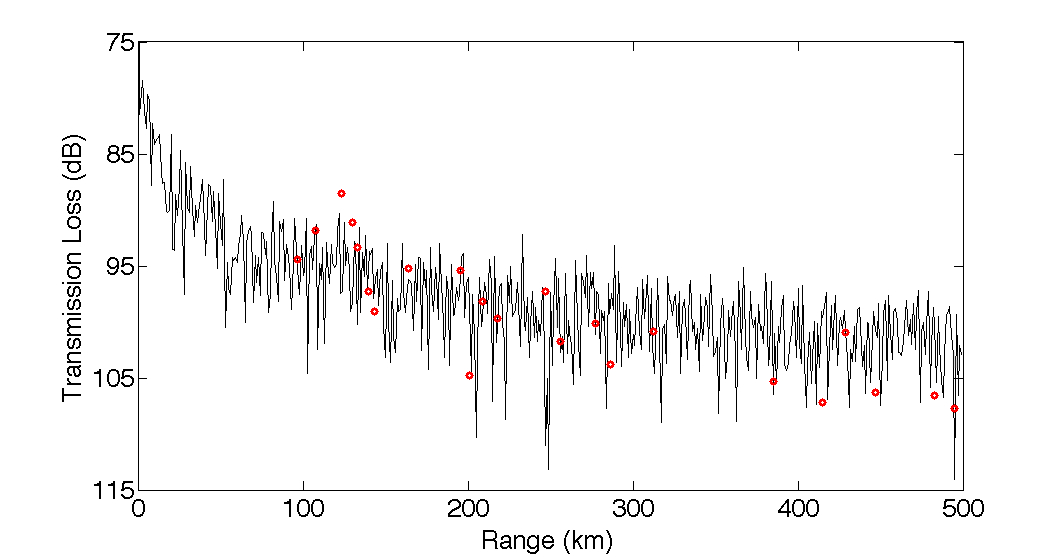
Figure 2: Transmission loss curves for the modified Pekeris waveguide (solid curve) compared to experimental data (red circles) for a receiver depth of 90 m and a 20 Hz sound source located at a depth of 243 m.
Waveguide propagation modeling techniques based on normal mode methods have been used previously to track endangered right whales in the Bering Sea [3]. For that particular environment, the Pekeris waveguide solution [4], a model developed by Pekeris in 1948 which modeled propagation in the Mediterranean and involved a liquid layer overlying a bottom sediment, was sufficient to model propagation characteristics. Further developments, such as those presented in the modified Pekeris waveguide, and inclusion of under-ice scattering loss, would be needed to adapt these techniques for tracking purposes in an Arctic environment. Both vocalizations and visual observations are used to count whales during migration. Long-term autonomous acoustic recording provides a means for monitoring whale calling activity in poor weather conditions and during periods in which ship-based visual and acoustic techniques are either impossible or cost prohibitive [3]. Combining these different techniques of experimental measurement and mathematical modeling allows for a more complete assessment of species numbers. An application of this work is to focus on using the solution derived in this work, with the required modifications to account for under-ice scattering loss, and received vocalization signals to determine distance to a calling whale, for example the endangered Arctic bowhead, that is used as a means to estimate minimum abundance for the species. Increased temperatures of Arctic waters are expected to result in increases in human activity (shipping, seismic exploration, oil exploration) in the region, which will in turn lead to higher noise levels. These increases in activity and noise are expected to influence the behavior and migration patterns of marine mammals in the Arctic. Waveguide modeling techniques are critical tools for modeling acoustics in this extreme environment and hence understanding effects on species living therein.
REFERENCES
[1] O.I. Diachok, “Effects of sea-ice ridges on sound propagation in the Arctic Ocean,” J. Acoust. Soc. Am. Vol. 59, 1110-1120 (1976).
[2] J.W. Wolf, O.I. Diachok, “Very-low-frequency under-ice reflectivity,” J. Acoust. Soc. Am. Vol. 93, 1329-1334 (1992).
[3] S.M. Wiggins, M.A. McDonald, L.M. Munger, S.E. Moore, J.A. Hildebrand, “Waveguide propagation allowsrange estimates for North Pacific right whales in the Bering Sea,” Canadian Acoustics Vol. 32, 146-154 (2004).
[4] C.L. Pekeris, “Theory of propagation of explosive sound in shallow water,” Geo. Soc. Am. Mem. 27 (1948).