Dr. P.G. Vaidya - vaidya@wsunix.wsu.edu
School of Mechanical and Material Engineering
Washington State University
Pullman, WA 99164
Popular version of paper 2pSPb1
presented Tuesday afternoon, 14 May 1996
ASA Meeting, Indianapolis, IN
Embargoed until 14 May 1996
I. Introduction
It is quite possible, that in a very near future, when you get a general physical examination, your doctor would try to find out whether your voice is chaotic. This is due to the fact that a strongly chaotic voice, in many cases, indicates the presence of various kinds of diseases.
However, this task is made a little more complicated by our discovery that even normal speech can display a different kind of chaos. The good news is that a careful measurement and analysis of this kind of chaos has the potential to serve as an early warning system for more serious chaos and possible onset of disease.
We have been able to simulate this chaos with a famous nonlinear equation, known as the Duffing's equation. By modulating the driving force, we could induce chaos, where none exists without the modulation. This chaos shares many of the characteristics of the chaos observed in normal human vowel sounds.
II. Background
The term "chaos" is a bit of a misnomer. As it is used by scientists today, a more accurate but less catchy phrase would be "co-evolution of order and disorder." A "periodic" signal exactly repeats itself over a fixed period. A "random" signal, on the other hand, never repeats itself and has no inner order. A chaotic signal, also does not repeat itself. However, it has subtle order which often could be well hidden.
It is often necessary to distinguish between these three types of signals. True randomness is so rare that the main task is often reduced to distinguishing between periodicity and chaos. One common method consists of finding the "Lyapunov exponents." This method consists of first converting the signal into a "state space," which can be seen as creating 3 or higher dimensional trajectories. Then, nearby trajectories are checked to see if they diverge from one another. If on the average over the entire space, they do, it is concluded that the signal is chaotic. The task is made a little harder if some extraneous noise contaminates the data. In this case, the computer program to calculate the exponents would require looking for trajectories which are at a distance which is larger than a specified distance, which depends upon an arbitrary estimate of the noise.
For theoretically generated simulations, it is possible to keep the extraneous noise to extremely small levels. Therefore, this method works quite well. However, virtually all experimental data, including the voice samples, are contaminated by noise.
It was therefore felt that a method to distinguish, in an unambiguous fashion, between periodicity and chaos was urgently needed. A method called Trans-Spectral Coherence or TSC, (Please see Vaidya, Anderson, JASA May 1991), had proved earlier to be especially successful in bringing out the hidden order in chaos. It also had led to further understanding of the mechanism of chaos. This method was modified to create a more sophisticated TSC called Mathew TSC or MTSC. The name Mathew was chosen because of a famous equation bearing the name, which plays an important role in the analysis which leads to Mathew TSC.
We have now proved that if ordinary TSC is low and MTSC is high it can only mean chaos. A Differential Trans-Spectrogram (informally named as the "Caseygram" by Vaidya) consists of the difference between these two TSC's, plotted as a function time and pitch.
The Caseygrams of normal voice samples showed many areas which clearly were chaotic. These results were reported at the St. Louis meeting of the Acoustical Society of America.
At this conference (in Indianapolis), we have another paper, (Comparison of Caseygrams for normal and pathological speech), in which we have analyzed data provided by Dr. Allison Behrman of the Cornell Medical Center in NY, which consists of voice samples from patients suffering from a unilateral polyp in the vocal apparatus. We have shown that as the disease progresses the Caseygrams show higher and higher values in the areas occupied by generally lower frequencies. We have also shown that even in the early stages, the Caseygrams give clear warnings that something is afoot.
III. Methods and Results:
We wanted to verify the hypothesis that phase modulation can induce this new type of a chaos. We used numerical solutions of the Duffing's equation to generate our results. We used the value of the forcing function which normally does not result into chaos. However, we modulated in turn, the driving amplitude, the phases and the driving frequency. All of these led to "induced chaos," in many cases. In some cases, periodic signals were seen and we also found intermittent chaos. Without the input of extraneous noise, all these could be equally well analyzed by Lyapunov method or by Caseygram. When the results were repeated with the addition of noise, only Caseygram gave unambiguous results.
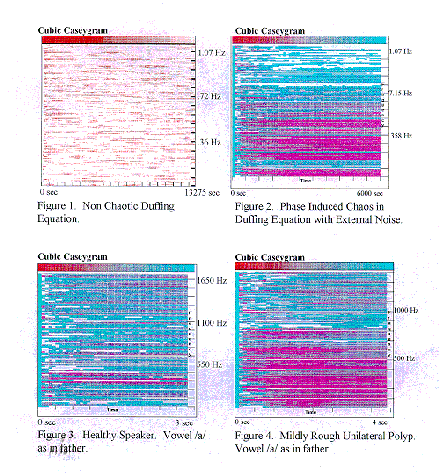
Figure 1 shows the Caseygram for the output of the Duffing's equation. There is no modulation. This picture is virtually free from chaos. The occasional slight positive values are very likely due to numerically generated input noise. Figure 2 shows an example of "induced chaos" due to phase modulation. Red (or dark) parts represent chaos. Figure 3 shows Caseygram of normal voice. It shows the presence of mini-chaos in normal voice. Figure 4 shows pathological voice and well developed chaos.
V. Discussion:
Why had the earlier researchers not found chaos in healthy vowel sounds? Our conclusion now is that this type of chaos is very heard to find by conventional methods. The signals differ from periodic signals by a very small magnitude. Even in a spectral analysis it shows up in the form of tiny subharmonics. These sub-harmonics could well be due to extraneous noise, and therefore conventional methods treat them as such. However, in Caseygram we unambiguously distinguish them from noise and periodicity and find that they are indeed chaotic.
We have concluded that this is a new form of chaos and by using a simulation shown that this could well be due to modulation.
Obviously the health implication of these results are of paramount importance to us. However, there is a somewhat lighter side to this work also. We always hear about a certain speaker having a "well modulated voice." We found that some modulations lead to more chaos than others.
Our hearing apparatus and the processing system in the brain must be at least as sophisticated as the Caseygrams. Probably a whole lot more!
The subharmonics, are known to give "timbre" to a person's voice. Now, perhaps we understand that mechanism that characterizes our voices ever so uniquely.
On a larger scale, the success at analyzing and predicting the onset of chaos in speech and its simulation by equations such as the Duffing's has enhanced the hope that we might be able to predict the onset of arrhythmia and heart attacks (which also give rise to chaotic signals) someday.