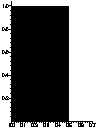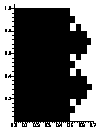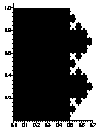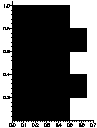
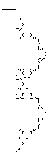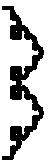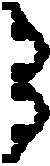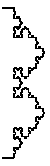Acoustical Society of America
ASA/EAA/DAGA '99 Meeting
Lay Language Papers


[ Lay Language Paper Index | Press Room ]

Fractal Modelling of Diffusive Urban Configurations

Philippe WOLOSZYN woloszyn@cerma.archi.fr
Laboratoire CERMA
UMR CNRS 1563
Ecole d'Architecture de Nantes
rue Massenet Nantes, 44300, France

Popular version of paper 4pNSc3
Presented Thursday Afternoon, March 18, 1999
ASA/EAA/DAGA '99 Meeting, Berlin, Germany

This research study, developed in the CERMA laboratory (UMR CNRS 1563), is part of the CNRS-Interdisciplinary Program for Towns " Sensitive towns ". Its aim, in collaboration with the LCPC, the LAUM (UMR CNRS 6613) and the CRESSON (UMR CNRS 1563), is to constitute a " Physical Organisation of the Acoustic Environment " model, called Orphea. The purpose of the presented research work is to evolve a transverse evaluation model of urban morphology in order to constitute a virtual sound simulation platform for urban soundscapes.

The fractal technique we develop for modelling the complexity of urban shapes quantifies discrete morphologies of the town with an automatic capture procedure based on Minkowski’s operators.

Therefore, the built structure is considered as a non-entire dimensional network, in order to define the diffusion capacity of the building for the acoustic field, the diffusion volume. This takes into account the volume implantation and the multiscale specular surface distribution in the urban space.

This will lead us to define the diffusion process as a geometrical-dependent phenomenon, confirming the rule of the built structure in urban acoustics.

The Minkowski fractal analysis

In order to model complex envelope configurations, we intend here to quantify the interface between built and non built structures of the street with fractal indicators, the multiscale relevance of which will allow the parametering of spectral diffuseness. Therefore, the morphological measurement of a fractal profile is presented to validate this indicator as a dilution measurement of built areas. For this purpose, we use a well-known fractal profile to simulate a growing complexity of the street, modelled from the Sierpinski Carpet. The inner dimensions are similar to the real street in which we measured the acoustic field, but its envelope changes from a totally smooth to a very rough configuration.

The fractal indicator of the totally iterated profile is easily calculated with two parameters of the iteration procedure, which are the reduction factor, indicating the length of the new segments at every iteration and the number of secondary segments for each iteration.

bonneaud1.gif (3166 octets)

Four steps of iteration of the Sierpinski profile (iteration 0 to iteration 3)

bonneaud2.gif (9843 octets)

Morphologic operation of Minkowski sausage applied on the last iteration of the Sierpinski profile

Every step of the evolution of this profile can be measured with the Minkowski Sausage method, which gives us the calculated value when applied on the totally iterated surface.

Practically, we replace each point of the profile with a disc. The union of all discs is called the Minkowski sausage, and the variation of the diameter of those discs gives us successive approached perimeters, the evolution of which constitutes the profile’s " Shape spectrum ", as shown following :

Image3.gif (3232 octets)

" Shape spectrum " from each step of iteration of the Sierpinski’s profile

This shape spectrum shows us how to parametrize a spatial diffusion : the diffusion frequency we work with is spatial, and defines the obstacles average number per length unit. L is the average distance between two obstacles for a given scale ; we call it localization length. This length corresponds to the upper limit which verifies the acoustic specular law, through the equality between the wave length of the incident sound l and the localization length of the built structure L.

The diffusion volume of a fractal structure

The diffusion volume is reducible to real convex isotropic Euclidean (non-fractal) structures, as polygons (for which it describes the real surface) and convex polyhedrons (for which it describes the effective volume). For all other cases where the structure presents a limit complexity, the diffusion volume describes the diffusion level of the structure, characterised with its topologic dimension d and its fractal dimension D.

Knowing that the volume V and the surface S of an Euclidean structure are defined with both quadratic and cubic relationships to the perimeter P with : S = Fq P et V = Fc P3, the geometrical nature of the entity is readable in the value of the prefactor in those relationships, the shape factors Fq and Fc.

Extending this expression to the structure's generalised volume Vx, those perimetric equations become, in the Euclidean system, Vx = Fx Pxd, or, for a D-dimensional fractal structure, Vx = Fx PxD.

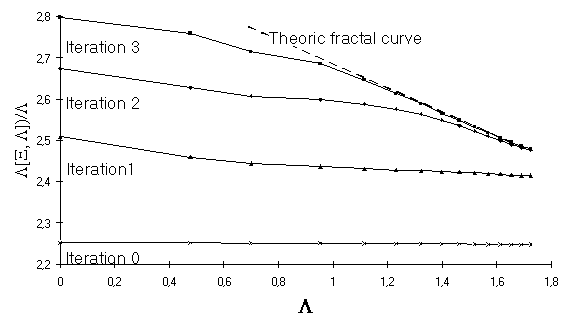
The prefactor Fx defines uniquely the global shape of the structure, Euclidean or fractal. The local shape complexity we quantify depends only on the perimeter power factor D, readable in the slope of the shape spectrum FD = d - D, which was estimated with the Minkowski recovering method, as shown previously.

For this Minkowski analysis of a continuous self-similar structure, such as the Sierpinski profile we saw before, the inferior and superior volumic measures of the structure converge to an eigenvalue involving simultaneously its local and global measures. This constitutes the measure of the diffusion volume of the structure. Its principle shows a dependence between the diffusion volume and both fractal and Euclidean dimensions D and d of the structure.

Frequency and diffusion coefficient

At the scale e, the specular limit of the acoustic propagation phenomena is expressed with the limit frequency fe, which wavelength le = c / fe corresponds to the lowest propagation mode, for the corresponding roughness of the structure, estimated with the localisation length L.

In this way, L represents the greatest distance for which the surface characterization is negligible compared to the wavelength   le.

Thus, the diffusion coefficient d is defined with its diffusive under-limit frequency fe, at the localization length L.

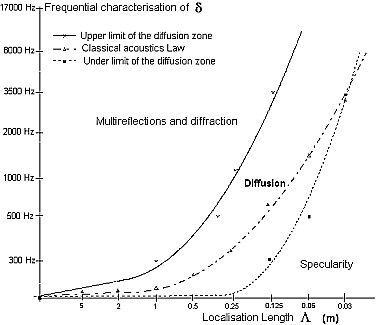
Image8.gif (10227 octets)

Frequency characterisation of the diffusion coefficient d, versus localization length L

For acoustic modes at frequencies greater than the wavelength le, acoustical propagation remains specular in the structure, which is classed as rigid for those frequencies : there is no diffusion.

Perspectives

The symmetry that appears between the number of reflections in a fractal structure and its localization length L allows us to reconsider the classical acoustic energy conservation laws.

The diffusion phenomenon model in a room considered as a self-similar network presents an important analogy with non ergodic structures, where preferred specular reflections directions do not allow an isotropic diffusion phenomenon.

Therefore, an urban street, assimilated to a one-sided open room, confirms this non-ergodicity, as the mean free path cannot be defined in that configuration. So it is possible to find specific diffusion modes, considering a typical energy behaviour in non-linear complex structures which exponent depends on the hyperbolic distribution process of the intermissions, the Levy flights.

Those flights are considered as infinite excursions, and the computation of their homothetic return probability allows us to parametrize their persistence, after have being " trapped " in the structure.

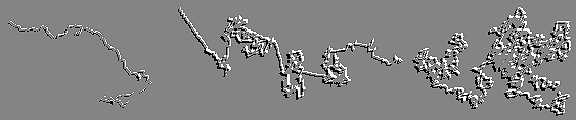
Image9.gif (7152 octets)

Three Levy flights, getting more and more persistent, from over- to under-diffusion

Those new acoustic hypothesis leads us to define another type of reverberation " over- ", or " under-diffusive ", depending on the fractal dimension D of the structure. Therefore, it would be necessary to define another energetic decreasing law, which would remain exponential: those perspectives constitute the next step of our research work.

References

  • D'Antonio P. : " Fractals and number theory ara changing the shape of acoustics ", Sound and Vibration, October 1992.
  • Frankhauser P., Sadler R. : " Fractal Analysis of Agglomerations ", in Sonderforschungsbereich 230 "Natrliche Konstruktionen", d. Natural Structures - Principles, Strategies and Models in Architecture and Nature, Vol.2, 1992.
  • Kuttruff H. : " A mathematical model for noise propagation between buildings ", J.Sound Vib. 85, 1982, pp.115-128.
  • Mandelbrot B. : " Les objets fractals ", Paris, Flammarion, 1992.
  • Woloszyn P., Raymond F., Picaut J. : " Morphological parametering of a diffusive acoustic model for complex urban areas ", in : Wesprac'97 6th Western Pacific regional acoustic conference, Hong-Kong, 19-21 novembre 1997. Hong Kong Institute of Acoustics, 1997, pp. 231-236
  • Woloszyn P. : " Caractrisation dimensionnelle de la diffusivit des formes architecturales urbaines ". Thse de doctorat de l'Universit de Nantes. 1998. 260 p.

[ Lay Language Paper Index | Press Room ]